题目内容
6.已知椭圆的长轴长是8,离心率是$\frac{3}{4}$,则此椭圆的标准方程是$\frac{x^2}{16}+\frac{y^2}{7}=1$或$\frac{x^2}{7}+\frac{y^2}{16}=1$.分析 由已知结合椭圆定义可得椭圆标准方程.
解答 解:由题意知,2a=8,∴a=4,
又$e=\frac{c}{a}=\frac{3}{4}$,∴c=3,
则b2=a2-c2=7.
当椭圆的焦点在x轴上时,椭圆方程为$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{7}=1$;
当椭圆的焦点在y轴上时,椭圆方程为$\frac{x^2}{7}+\frac{y^2}{16}=1$.
故答案为:$\frac{x^2}{16}+\frac{y^2}{7}=1$或$\frac{x^2}{7}+\frac{y^2}{16}=1$.
点评 本题考查椭圆的简单性质,考查椭圆方程的求法,是基础题.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
10.若α∈(0,π),且sinα+cosα=-$\frac{\sqrt{3}}{3}$,则α的取值范围是( )
| A. | (0,$\frac{π}{2}$) | B. | ($\frac{π}{2}$,π) | C. | ($\frac{π}{2}$,$\frac{3π}{4}$) | D. | ($\frac{3π}{4}$,π) |
14.若tan(π+α)=3,则sin(-α)cos(π-α)=( )
| A. | $-\frac{3}{10}$ | B. | $\frac{3}{10}$ | C. | $-\frac{1}{10}$ | D. | $\frac{1}{10}$ |
1.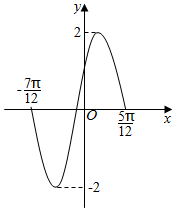 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,则下列判断错误的是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,则下列判断错误的是( )
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,则下列判断错误的是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,则下列判断错误的是( )| A. | A=2 | B. | ω=2 | C. | f(0)=1 | D. | φ=$\frac{5π}{6}$ |
18.已知椭圆$C:\frac{x^2}{4}+{y^2}=1,A({2,0})$,点P在椭圆C上,且OP⊥PA,其中O为坐标原点,则点P的坐标为( )
| A. | $({\frac{2}{3},±\frac{{2\sqrt{2}}}{3}})$ | B. | $({\frac{{2\sqrt{5}}}{3},±\frac{2}{3}})$ | C. | $({-\frac{2}{3},±\frac{{2\sqrt{2}}}{3}})$ | D. | $({-\frac{{2\sqrt{5}}}{3},±\frac{2}{3}})$ |
15.设Sn是等差数列{an}的前n项和,若a2+a3+a4=3,则S5=( )
| A. | 5 | B. | 7 | C. | 9 | D. | 11 |