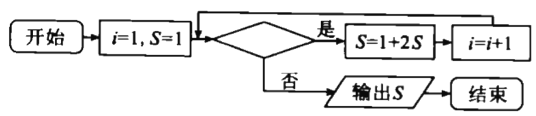
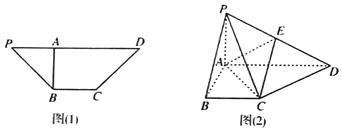
题目内容
【题目】在平面上,给定非零向量![]() ,对任意向量
,对任意向量![]() ,定义
,定义![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() ;
;
(2)若![]() ,证明:若位置向量
,证明:若位置向量![]() 的终点在直线
的终点在直线![]() 上,则位置向量
上,则位置向量![]() 的终点也在一条直线上;
的终点也在一条直线上;
(3)已知存在单位向量![]() ,当位置向量
,当位置向量![]() 的终点在抛物线
的终点在抛物线![]() :
:![]() 上时,位置向量
上时,位置向量![]() 终点总在抛物线
终点总在抛物线![]() :
:![]() 上,曲线
上,曲线![]() 和
和![]() 关于直线
关于直线![]() 对称,问直线
对称,问直线![]() 与向量
与向量![]() 满足什么关系?
满足什么关系?
【答案】(1)![]() (2)见证明 (3)直线
(2)见证明 (3)直线![]() 与向量
与向量![]() 垂直
垂直
【解析】
(1)根据题意,算出![]() 7,
7,![]() 10,代入
10,代入![]() 的表达式并化简整理,即可得到
的表达式并化简整理,即可得到![]() (
(![]() ,
,![]() );(2)设
);(2)设![]() (x',y'),终点在直线Ax+By+C=0上,由题中
(x',y'),终点在直线Ax+By+C=0上,由题中![]() 的表达式解出
的表达式解出![]() (x,y)满足的关系式,从而得到点(
(x,y)满足的关系式,从而得到点(![]() ,
,![]() )在直线Ax+By+C=0上,化简整理得到直线(3A+4B)x+(4A﹣3B)y﹣5C=0,说明向量
)在直线Ax+By+C=0上,化简整理得到直线(3A+4B)x+(4A﹣3B)y﹣5C=0,说明向量![]() 的终点也在一条直线上;(3)设
的终点也在一条直线上;(3)设![]() ,则
,则![]() ,取
,取![]() ,解出
,解出![]() 关于
关于![]() 和t的坐标形式,结合
和t的坐标形式,结合![]() 的终点在抛物线x2=y上且
的终点在抛物线x2=y上且![]() 终点在抛物线y2=x上,建立关于
终点在抛物线y2=x上,建立关于![]() 和t的方程,化简整理得到
和t的方程,化简整理得到![]() ±(
±(![]() ,
,![]() ).再由曲线C和C′关于直线l:y=x对称,算出l的方向向量
).再由曲线C和C′关于直线l:y=x对称,算出l的方向向量![]() 满足
满足![]()
![]() 0,从而得到直线l与向量
0,从而得到直线l与向量![]() 垂直.
垂直.
(1)根据题意,![]() 7,
7,![]() 10,∴
10,∴![]() .
.
(2)设![]() ,
,![]() ,则
,则
![]()
![]() ,
,
∴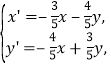
于是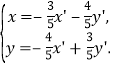 故
故![]() ,
,
从而![]() ,
,
由于![]() 、
、![]() 不全为零,所以
不全为零,所以![]() ,
,![]() 也不全为零.
也不全为零.
于是![]() 的终点在直线
的终点在直线![]() 上.
上.
(3)设![]() ,则
,则![]() ,对任意实数
,对任意实数![]() ,取
,取![]() ,
,
则![]()
![]()
![]() ,
,
∵![]() 的终点在曲线
的终点在曲线![]() 上,
上,
∴![]() .①
.①
由于![]() 为任意实数,比较①式两边
为任意实数,比较①式两边![]() 的系数得
的系数得
![]() ,
,![]() ,
,![]() ,
,
从而![]() ,
,![]() ,
,
∴![]() .
.
对曲线![]() 中任意点
中任意点![]() ,可知
,可知![]() 落在曲线
落在曲线![]() 上,反之亦然,故曲线
上,反之亦然,故曲线![]() :
:![]() 与曲线
与曲线![]() :
:![]() 关于直线
关于直线![]() :
:![]() 对称,
对称,
![]() 的方向向量
的方向向量![]() ,∵
,∵![]() ,∴
,∴![]() ,即直线
,即直线![]() 与向量
与向量![]() 垂直.
垂直.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目