题目内容
如图,在平面直角坐标系xOy中,椭圆 的离心率为
的离心率为 ,过椭圆右焦点
,过椭圆右焦点 作两条互相垂直的弦
作两条互相垂直的弦 与
与 .当直线
.当直线 斜率为0时,
斜率为0时, .
.

(1)求椭圆的方程;
(2)求 的取值范围.
的取值范围.
 的离心率为
的离心率为 ,过椭圆右焦点
,过椭圆右焦点 作两条互相垂直的弦
作两条互相垂直的弦 与
与 .当直线
.当直线 斜率为0时,
斜率为0时, .
.
(1)求椭圆的方程;
(2)求
 的取值范围.
的取值范围.(1) ,(2)
,(2)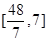 .
.
 ,(2)
,(2)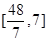 .
.试题分析:(1)求椭圆标准方程,只需两个独立条件. 一个是
 ,另一个是点
,另一个是点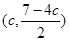 在椭圆上即
在椭圆上即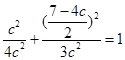 ,所以
,所以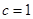 .所以椭圆的方程为
.所以椭圆的方程为 .(2)研究直线与椭圆位置关系,关键确定参数,一般取直线的斜率,① 当两条弦中一条斜率为0时,另一条弦的斜率不存在,由题意知
.(2)研究直线与椭圆位置关系,关键确定参数,一般取直线的斜率,① 当两条弦中一条斜率为0时,另一条弦的斜率不存在,由题意知 ,② 当两弦斜率均存在且不为0时,设直线
,② 当两弦斜率均存在且不为0时,设直线 的方程为
的方程为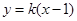 ,将直线
,将直线 的方程代入椭圆方程中,并整理得
的方程代入椭圆方程中,并整理得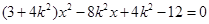 ,所以
,所以 .同理,
.同理, .所以
.所以 ,利用不等式或函数单调性可得
,利用不等式或函数单调性可得 的取值范围是
的取值范围是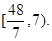 综合①与②可知,
综合①与②可知, 的取值范围是
的取值范围是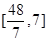 .
.【解】(1)由题意知,
 ,
, ,
,所以
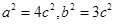 . 2分
. 2分因为点
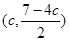 在椭圆上,即
在椭圆上,即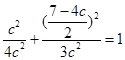 ,
,所以
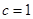 .
.所以椭圆的方程为
 . 6分
. 6分(2)① 当两条弦中一条斜率为0时,另一条弦的斜率不存在,
由题意知
 ; 7分
; 7分② 当两弦斜率均存在且不为0时,设
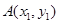 ,
,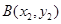 ,
,且设直线
 的方程为
的方程为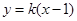 ,
,则直线
 的方程为
的方程为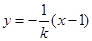 .
.将直线
 的方程代入椭圆方程中,并整理得
的方程代入椭圆方程中,并整理得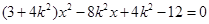 ,
,所以
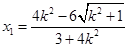 ,
,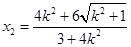 ,
,所以
 . 10分
. 10分同理,
 .
.所以
 , 12分
, 12分令
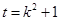 ,则
,则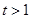 ,
,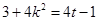 ,
,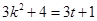 ,
,设
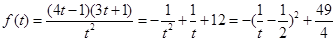 ,
,因为
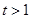 ,所以
,所以 ,
,所以
 ,
,所以
 .
.综合①与②可知,
 的取值范围是
的取值范围是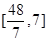 . 16分
. 16分
练习册系列答案
相关题目
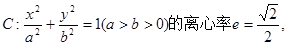 左、右焦点分别为F1、F2,点P(2,
左、右焦点分别为F1、F2,点P(2,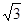 ),点F2在线段PF1的中垂线上.
),点F2在线段PF1的中垂线上.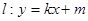 与椭圆C交于M、N两点,直线F2M与F2N的斜率互为相反数,求证:直线l过定点,并求该定点的坐标.
与椭圆C交于M、N两点,直线F2M与F2N的斜率互为相反数,求证:直线l过定点,并求该定点的坐标.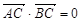 ,|BC|=2|AC|.
,|BC|=2|AC|.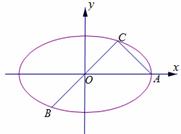
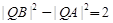 ?若存在,有几个(不必求出Q点的坐标),若不存在,请说明理由.
?若存在,有几个(不必求出Q点的坐标),若不存在,请说明理由.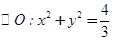 的两条切线,切点分别为M、N,若直线MN在x轴、y轴上的截距分别为m、n,证明:
的两条切线,切点分别为M、N,若直线MN在x轴、y轴上的截距分别为m、n,证明: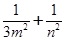 为定值.
为定值. 和椭圆
和椭圆 有相同的焦点,且双曲线的离心率是椭圆离心率的两倍,则双曲线的方程为 _________ .
有相同的焦点,且双曲线的离心率是椭圆离心率的两倍,则双曲线的方程为 _________ . 分别是椭圆:
分别是椭圆: 的左、右焦点,过
的左、右焦点,过 倾斜角为
倾斜角为 的直线
的直线 与该椭圆相交于P,
与该椭圆相交于P, 两点,且
两点,且 .则该椭圆的离心率为( )
.则该椭圆的离心率为( )


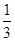
 内接于椭圆
内接于椭圆 ,且
,且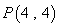 ,圆C:
,圆C: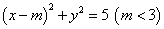 与椭圆E:
与椭圆E: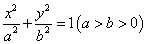 有一个公共点
有一个公共点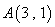 ,
,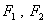 分别是椭圆的左、右焦点,直线
分别是椭圆的左、右焦点,直线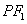 与圆C相切.
与圆C相切.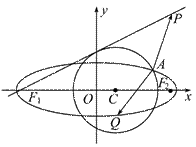
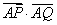 的取值范围.
的取值范围. 上一点
上一点 到焦点
到焦点 的距离为6,则点
的距离为6,则点 的距离为( )
的距离为( ) 的右焦点为
的右焦点为 ,椭圆
,椭圆 与
与 轴正半轴交于
轴正半轴交于 点,与
点,与 轴正半轴交于
轴正半轴交于 ,且
,且 ,过点
,过点 作直线
作直线 交椭圆于不同两点
交椭圆于不同两点 ,则直线
,则直线


