题目内容
设
分别是椭圆：
的左、右焦点，过
倾斜角为
的直线
与该椭圆相交于P，
两点，且
.则该椭圆的离心率为（ ）
分别是椭圆：的左、右焦点，过倾斜角为的直线与该椭圆相交于P，两点，且.则该椭圆的离心率为（ ）A． | B． | C． | D． |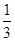
B
直线
斜率为1，设直线的方程为
，其中
.
设
，则
两点坐标满足方程组
化简得
，则
，
因为，所以
.
得
，故
，
所以椭圆的离心率
，选B.
斜率为1，设直线的方程为，其中.设
，则两点坐标满足方程组化简得，则，因为，所以
.得
，故，所以椭圆的离心率
，选B.
练习册系列答案
特高级教师点拨系列答案
相关题目
的左、右焦点分别为
，其上顶点为
已知
是边长为
的正三角形．
的方程；
任作一动直线
交椭圆
两点，记
．若在线段
上取一点
，使得
，当直线
与椭圆
相交于
两点，点
是线段
上的一点，
且点
上.
的对称点在单位圆
上，求椭圆的方程.
：
（
）过点
，且椭圆
．
在直线
上，过
两点，且
中点，再过
．求直线
是否恒过定点，如果是则求出该定点的坐标，不是请说明理由。
，过点
且离心率为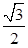
.
的方程；
是椭圆
，连接AM交椭圆于点P，在x轴上是否存在异于A、B的定点Q,使得直线BP和直线MQ垂直.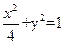
截得的最大弦长等于( )
的离心率为
，过椭圆右焦点
作两条互相垂直的弦
与
．当直线
．
的取值范围．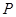
是椭圆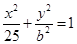
,
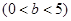上除顶点外的一点，
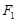是椭圆的左焦点，若
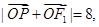则点
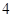
的中心和左焦点，点P为椭圆上的任意一点，则
的最大值为（ ）