题目内容
如图所示,已知A、B、C是长轴长为4的椭圆E上的三点,点A是长轴的一个端点,BC过椭圆中心O,且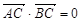 ,|BC|=2|AC|.
,|BC|=2|AC|.
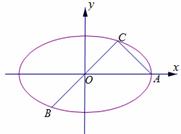
(1)求椭圆E的方程;
(2)在椭圆E上是否存点Q,使得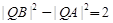 ?若存在,有几个(不必求出Q点的坐标),若不存在,请说明理由.
?若存在,有几个(不必求出Q点的坐标),若不存在,请说明理由.
(3)过椭圆E上异于其顶点的任一点P,作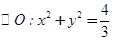 的两条切线,切点分别为M、N,若直线MN在x轴、y轴上的截距分别为m、n,证明:
的两条切线,切点分别为M、N,若直线MN在x轴、y轴上的截距分别为m、n,证明: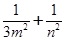 为定值.
为定值.
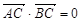 ,|BC|=2|AC|.
,|BC|=2|AC|.
(1)求椭圆E的方程;
(2)在椭圆E上是否存点Q,使得
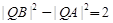 ?若存在,有几个(不必求出Q点的坐标),若不存在,请说明理由.
?若存在,有几个(不必求出Q点的坐标),若不存在,请说明理由.(3)过椭圆E上异于其顶点的任一点P,作
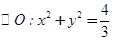 的两条切线,切点分别为M、N,若直线MN在x轴、y轴上的截距分别为m、n,证明:
的两条切线,切点分别为M、N,若直线MN在x轴、y轴上的截距分别为m、n,证明: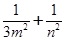 为定值.
为定值.(1)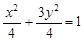 ;(2)满足条件的点Q存在,且有两个.
;(2)满足条件的点Q存在,且有两个.
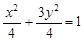 ;(2)满足条件的点Q存在,且有两个.
;(2)满足条件的点Q存在,且有两个.试题分析:本题主要考查椭圆的标准方程及其性质,考查学生的转化思想和数形结合思想,考查分析问题解决问题的能力和计算能力.第一问,先由长轴长得到a的值,设出椭圆的标准方程,利用已知条件数形结合得到C点坐标,将C点坐标代入到椭圆中,得到b的值,从而得到椭圆的标准方程;第二问,先设出Q点坐标,利用已知等式计算,可知点Q在直线
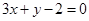 上,点
上,点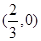 在直线上,而在椭圆内部,数形结合得存在点Q而且存在2个;法二:用
在直线上,而在椭圆内部,数形结合得存在点Q而且存在2个;法二:用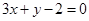 和椭圆方程联立消参,得到关于x的方程,看方程的判别式,判别式大于0时,方程有2个根,则直线与椭圆有2个交点;第三问,设出点P的坐标,由切线的性质得四点共圆,此圆的圆心为
和椭圆方程联立消参,得到关于x的方程,看方程的判别式,判别式大于0时,方程有2个根,则直线与椭圆有2个交点;第三问,设出点P的坐标,由切线的性质得四点共圆,此圆的圆心为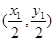 ,直径为OP,得到此圆的方程,M、N既在此圆上,又在圆O上,2个方程联立,解出直线MN的方程,得出截距的值,再转化出P点坐标代入到椭圆中即可;法二:设出点P、M、N的坐标,利用直线的垂直关系,利用斜率列出等式,转化成直线PM和直线PN的方程,从而得到直线MN的方程.
,直径为OP,得到此圆的方程,M、N既在此圆上,又在圆O上,2个方程联立,解出直线MN的方程,得出截距的值,再转化出P点坐标代入到椭圆中即可;法二:设出点P、M、N的坐标,利用直线的垂直关系,利用斜率列出等式,转化成直线PM和直线PN的方程,从而得到直线MN的方程.试题解析:(1)依题意知:椭圆的长半轴长
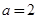 ,则A(2,0),
,则A(2,0),设椭圆E的方程为
 2分
2分由椭圆的对称性知|OC|=|OB|又∵
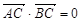 ,|BC|=2|AC|
,|BC|=2|AC|∴AC⊥BC,|OC|=|AC|∴△AOC为等腰直角三角形,
∴点C的坐标为(1,1),点B的坐标为(-1,-1), 4分
将C的坐标(1,1)代入椭圆方程得
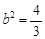
∴所求的椭圆E的方程为
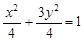 5分
5分(2)解法一:设在椭圆E上存在点Q,使得
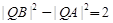 ,设
,设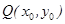 ,则
,则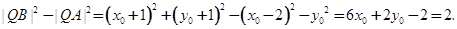
即点Q在直线
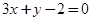 上, 7分
上, 7分∴点Q即直线
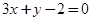 与椭圆E的交点,
与椭圆E的交点,∵直线
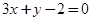 过点
过点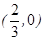 ,而点椭圆
,而点椭圆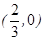 在椭圆E的内部,
在椭圆E的内部,∴满足条件的点Q存在,且有两个. 9分
解法二:设在椭圆E上存在点Q,使得
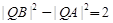 ,设
,设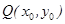 ,则
,则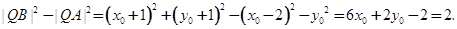
即
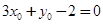 , ① -7分
, ① -7分又∵点Q在椭圆E上,∴
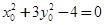 , ②
, ②由①式得
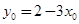 代入②式并整理得:
代入②式并整理得: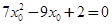 , -③
, -③∵方程③的根判别式
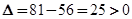 ,
,∴方程③有两个不相等的实数根,即满足条件的点Q存在,且有两个. 9分
(3)解法一:
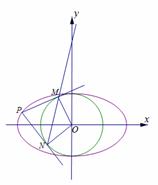
设点
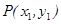 ,由M、N是
,由M、N是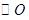 的切点知,
的切点知,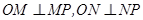 ,
,∴O、M、P、N四点在同一圆上, 10分
且圆的直径为OP,则圆心为
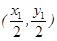 ,
,其方程为
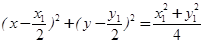 , 11分
, 11分即
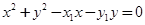 -④
-④即点M、N满足方程④,又点M、N都在
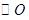 上,
上,∴M、N坐标也满足方程
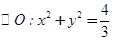 -⑤
-⑤⑤-④得直线MN的方程为
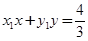 , 12分
, 12分令
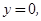 得
得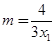 ,令
,令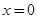 得
得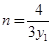 , 13分
, 13分∴
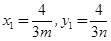 ,又点P在椭圆E上,
,又点P在椭圆E上,∴
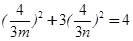 ,即
,即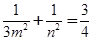 =定值. 14分
=定值. 14分解法二:设点
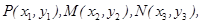 则
则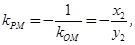 10分
10分直线PM的方程为
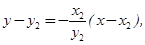 化简得
化简得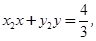 ④
④同理可得直线PN的方程为
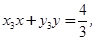 -⑤ 11分
-⑤ 11分把P点的坐标代入④、⑤得
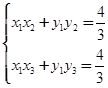
∴直线MN的方程为
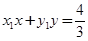 , 12分
, 12分令
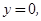 得
得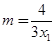 ,令
,令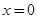 得
得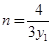 , 13分
, 13分∴
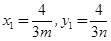 ,又点P在椭圆E上,
,又点P在椭圆E上,∴
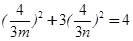 ,即
,即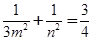 =定值. -14分
=定值. -14分
练习册系列答案
相关题目
 和
和 ,圆
,圆 是以
是以 的圆,点
的圆,点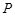 是圆
是圆 的垂直平分线
的垂直平分线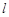 和半径
和半径 所在的直线交于点
所在的直线交于点 .
.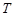 ;
; ,
, 是曲线
是曲线 (
( 为坐标原点),求实数
为坐标原点),求实数 的取值范围.
的取值范围. 的焦距为
的焦距为 ,过右焦点和短轴一个端点的直线的斜率为
,过右焦点和短轴一个端点的直线的斜率为 ,
, 为坐标原点.
为坐标原点. 的方程.
的方程. 的直线
的直线 与
与 、
、 两点,记
两点,记 面积的最大值为
面积的最大值为 ,证明:
,证明: .
. 的离心率为
的离心率为 ,过椭圆右焦点
,过椭圆右焦点 作两条互相垂直的弦
作两条互相垂直的弦 与
与 .当直线
.当直线 .
.
 的取值范围.
的取值范围.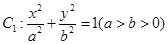 与圆
与圆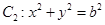 ,若在椭圆
,若在椭圆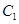 上存在点P,使得由点P所作的圆
上存在点P,使得由点P所作的圆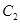 的两条切线互相垂直,则椭圆
的两条切线互相垂直,则椭圆
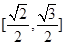


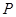 是椭圆
是椭圆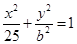 ,
,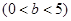 上除顶点外的一点,
上除顶点外的一点,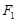 是椭圆的左焦点,若
是椭圆的左焦点,若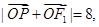 则点
则点
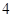


 与
与 的曲线大致是( )
的曲线大致是( )
 =1(a>b>0)的一个顶点为A(2,0),离心率为
=1(a>b>0)的一个顶点为A(2,0),离心率为 .直线y=k(x-1)与椭圆C交于不同的两点M,N.
.直线y=k(x-1)与椭圆C交于不同的两点M,N. 时,求k的值.
时,求k的值. ,
, 是双曲线
是双曲线 :
: 与椭圆
与椭圆 的公共焦点,点
的公共焦点,点 是
是 ,
, 在第一象限的公共点.若|F1F2|=|F1A|,则
在第一象限的公共点.若|F1F2|=|F1A|,则



