题目内容
【题目】如图,![]() 的内心为
的内心为![]() ,
,![]() 、
、![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 、
、![]() 的中点,证明:直线
的中点,证明:直线![]() 平分
平分![]() 的周长.
的周长.
【答案】见解析
【解析】
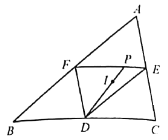
如图①,不妨设![]() ,
,![]() 的内切圆切
的内切圆切![]() 、
、![]() 、
、![]() 于
于![]() 、
、![]() 、
、![]() .
.

图①
过![]() 作内切圆的直径
作内切圆的直径![]() ,过
,过![]() 作
作![]() 的切线分别交
的切线分别交![]() 、
、![]() 于
于![]() 、
、![]() ,则
,则![]() .
.
由于![]() 是
是![]() 的旁切圆,
的旁切圆,![]() ,因
,因![]() ,
,![]() ,
,
所以有![]() .
.
延长![]() 交
交![]() 于
于![]() ,则
,则![]() ,因此
,因此![]() ,
,
故![]() 是
是![]() 的中位线,所以
的中位线,所以![]() ,
,
因四边形![]() 为平行四边形,所以
为平行四边形,所以![]() ∽
∽![]() ,相似比为
,相似比为![]() .
.
同理,![]() ∽
∽![]() ,相似比为
,相似比为![]() .
.
又注意![]() ∽
∽![]() ,
,![]() ∽
∽![]() ,相似比均为
,相似比均为![]() ,
,
既然有![]() ,所以
,所以![]() ,
,
因此,![]() ,即所证结论成立.
,即所证结论成立.
附注 在几何题中用到三角形内切圆的一个基本性质.
如图②,在![]() 中,内切圆
中,内切圆![]() 切
切![]() 于
于![]() ,
,
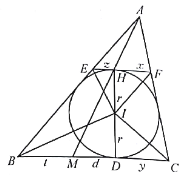
设![]() 是
是![]() 的直径,若
的直径,若![]() 交
交![]() 于
于![]() ,则
,则![]() .
.
证明:过![]() 作
作![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上.
上.
设![]() 的半径为
的半径为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
连结![]() 、
、![]() 、
、![]() 、
、![]() ,由于
,由于![]() 、
、![]() 分别平分一对互补角
分别平分一对互补角![]() 、
、![]() ,
,
所以![]() ,且
,且![]() ∽
∽![]() ,则
,则![]() ,
,![]() .
.
同理![]() ∽
∽![]() ,则
,则![]() ,
,![]() ,
,
所以![]() ,则
,则![]() . ①
. ①
又由![]() ,得
,得![]() ,所以
,所以![]() , ②
, ②
根据①②式得,![]() ,所以
,所以![]() ,即
,即![]() ,
,
由此得,![]() ,即
,即![]() ,也就是
,也就是![]() .(同时也有
.(同时也有![]() .)
.)

练习册系列答案
相关题目