题目内容
10．（Ⅰ）计算：${（{\sqrt{2}-1}）^0}-\sqrt{\frac{1}{{4×{3^2}}}}+\frac{1}{{{2^2}×\sqrt{2+{2^{-2}}}}}$；（Ⅱ）若tanx=2，求值：$\frac{2sin（π-x）-cosx}{{cosx-cos（\frac{3π}{2}-x）}}$．
分析 （Ⅰ）由条件利用分数指数幂的运算法则求得要求式子的值．
（Ⅱ）由条件利用同角三角函数的基本关系，求得要求式子的值．
解答 （Ⅰ）解：${（{\sqrt{2}-1}）^0}-\sqrt{\frac{1}{{4×{3^2}}}}+\frac{1}{{{2^2}×\sqrt{2+{2^{-2}}}}}$=1-$\frac{1}{6}$+$\frac{1}{4•\frac{3}{2}}$=1．
（Ⅱ）解：∵tanx=2，∴$\frac{2sin（π-x）-cosx}{{cosx-cos（\frac{3π}{2}-x）}}$=$\frac{2sinx-cosx}{cosx+sinx}=\frac{2tanx-1}{1+tanx}=\frac{2×2-1}{1+2}=1$．
点评 本题主要考查分数指数幂的运算法则，同角三角函数的基本关系，属于基础题．
练习册系列答案
小博士期末闯关100分系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
已知函数f（x）是定义在R上的偶函数，当x≥0时，f（x）=x（x-2）．
1．$\frac{{\sqrt{3}-tan{{15}^0}}}{{\sqrt{3}tan{{15}^0}+1}}$=（ ）
| A． | -1 | B． | $\frac{{\sqrt{3}}}{3}$ | C． | 1 | D． | $\sqrt{3}$ |
5．
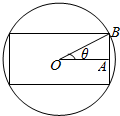把截面半径为5的圆形木头锯成面积为y的矩形木料，如图，点O为圆心，OA⊥OB，设∠AOB=θ，把面积y表示为θ的表达式，则有（ ）
把截面半径为5的圆形木头锯成面积为y的矩形木料，如图，点O为圆心，OA⊥OB，设∠AOB=θ，把面积y表示为θ的表达式，则有（ ）| A． | y=50cos2θ | B． | y=25sinθ | C． | y=25sin2θ | D． | y=50sin2θ |
15．若cosθ=$\frac{3}{5}$（-$\frac{π}{2}$＜θ＜0），则cos（θ-$\frac{π}{6}$）的值是（ ）
| A． | $\frac{3\sqrt{3}±4}{10}$ | B． | $\frac{4±3\sqrt{3}}{10}$ | C． | $\frac{3\sqrt{3}-4}{10}$ | D． | $\frac{3\sqrt{3}+4}{10}$ |