题目内容
 的展开式中,
的展开式中, 的系数可以表示从
的系数可以表示从 个不同物体中选出
个不同物体中选出 个的方法总数.下列各式的展开式中
个的方法总数.下列各式的展开式中 的系数恰能表示从重量分别为
的系数恰能表示从重量分别为 克的砝码(每种砝码各一个)中选出若干个,使其总重量恰为
克的砝码(每种砝码各一个)中选出若干个,使其总重量恰为 克的方法总数的选项是()
克的方法总数的选项是()
A.
B.
C.
D.
【答案】
A
【解析】
试题分析:对于这10个砝码而言,只有选与不选的区别。
对于重量为n的砝码,选择了它,则它对 中的指数8的贡献为n,在代数式中即为
中的指数8的贡献为n,在代数式中即为 ;
;
如果没有选择该砝码,则它对 中的指数8的贡献为0,在代数式中即为
中的指数8的贡献为0,在代数式中即为 =1,
=1, 可以看成(
可以看成( +x)(
+x)( +
+ )(
)( +
+ )灬(
)灬( +
+ ),在上述的代数式子相乘的过程中即为从每个独立的代数式
),在上述的代数式子相乘的过程中即为从每个独立的代数式 +
+ 中的2个项任意选择一个相乘(选择一个就是代表每个砝码的选择与否),最后将这些相乘的结果相加合并同类项,在每个独立的代数式
中的2个项任意选择一个相乘(选择一个就是代表每个砝码的选择与否),最后将这些相乘的结果相加合并同类项,在每个独立的代数式 +
+ 中的2个项任意选择一个相乘的过程中如果得到
中的2个项任意选择一个相乘的过程中如果得到 ,则这就是一种总重量恰为8克的方法,故选A。
,则这就是一种总重量恰为8克的方法,故选A。
考点:组合数公式,组合的应用。
点评:中档题,关键是将问题加以转化,转化成二项式的展开问题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 展开式中含
展开式中含 的项.,并指出这一项的二项式系数。
的项.,并指出这一项的二项式系数。 可看成是以r为自变量的函数f(r),其定义域是{r|r∈N,r≤n}.
可看成是以r为自变量的函数f(r),其定义域是{r|r∈N,r≤n}. ;
; 展开式中含
展开式中含 的项.,并指出这一项的二项式系数。
的项.,并指出这一项的二项式系数。 可看成是以r为自变量的函数f(r),其定义域是{r|r∈N,r≤n}.
可看成是以r为自变量的函数f(r),其定义域是{r|r∈N,r≤n}.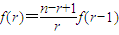 ;
;