题目内容
从函数角度看,组合数
可看成是以r为自变量的函数f(r),其定义域是{r|r∈N,r≤n}.
(1)证明:f(r)=
f(r-1);
(2)利用(1)的结论,证明:当n为偶数时,(a+b)n的展开式中最中间一项的二项式系数最大.
| C | r n |
(1)证明:f(r)=
| n-r+1 |
| r |
(2)利用(1)的结论,证明:当n为偶数时,(a+b)n的展开式中最中间一项的二项式系数最大.
分析:(1)先根据组合数公式求出f(r)、f(r-1),计算
•f(r-1)的值,从而证得结论.
(2)设n=2k,k∈z,由(1)可得
=
,令f(r)≥f(r-1),可得r≤k+
(等号不成立).故有当r=1,2,3…k时,f(r)>f(r-1)成立;当r=k+1,k+2,k+33…2k时,f(r)<f(r-1)成立.故f(k)=
最大,从而证得结论.
| n-r+1 |
| r |
(2)设n=2k,k∈z,由(1)可得
| f(r) |
| f(r-1) |
| 2k-r+1 |
| r |
| 1 |
| 2 |
| C | k 2k |
解答:(1)证明:∵f(r)=
=
,而 f(r-1)=
=
,
∴
•f(r-1)=
•
=
,
故f(r)=
f(r-1)成立.
(2)证明:当n为偶数时,设n=2k,k∈z,∵f(r)=
f(r-1),f(r-1)>0.
∴
=
.
令f(r)≥f(r-1),可得
≥1,∴r≤k+
(等号不成立).
∴当r=1,2,3…k时,f(r)>f(r-1)成立;
反之,当r=k+1,k+2,k+3…2k时,f(r)<f(r-1)成立.
故f(k)=
最大,即(a+b)n的展开式中最中间一项的二项式系数最大.
| C | r n |
| n! |
| r!•(n-r)! |
| C | r-1 n |
| n! |
| (r-1)!•(n-r+1)! |
∴
| n-r+1 |
| r |
| n-r+1 |
| r |
| n! |
| (r-1)!•(n-r+1)! |
| n! |
| r!•(n-r)! |
故f(r)=
| n-r+1 |
| r |
(2)证明:当n为偶数时,设n=2k,k∈z,∵f(r)=
| n-r+1 |
| r |
∴
| f(r) |
| f(r-1) |
| 2k-r+1 |
| r |
令f(r)≥f(r-1),可得
| 2k-r+1 |
| r |
| 1 |
| 2 |
∴当r=1,2,3…k时,f(r)>f(r-1)成立;
反之,当r=k+1,k+2,k+3…2k时,f(r)<f(r-1)成立.
故f(k)=
| C | k 2k |
点评:本题主要考查组合及组合数公式,二项式定理的应用以及二项式系数的性质,属于基础题.

练习册系列答案
相关题目
 可看成是以r为自变量的函数f(r),其定义域是{r|r∈N,r≤n}.
可看成是以r为自变量的函数f(r),其定义域是{r|r∈N,r≤n}. ;
; 可看成是以r为自变量的函数f(r),其定义域是{r|r∈N,r≤n}.
可看成是以r为自变量的函数f(r),其定义域是{r|r∈N,r≤n}.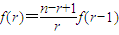 ;
;