题目内容
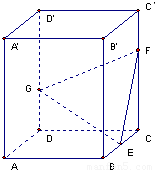
若四棱柱ABCD-A1B1C1D1的底面是边长为1的正方形，且侧棱垂直于底面，若AB1与底面ABCD成60°角，则二面角C-B1D1-C1的平面角的正切值为
______．
因为B1B⊥底面ABCD，所以AB1与底面ABCD成的角为∠B1AB，由∠B1AB=60°得B1B=
，
因为C1C⊥底面A1B1C1D1，连接A1C1，交B1D1与O，则C1O⊥B1D1，
连接CO，则∠C1OC即为二面角C-B1D1-C1的平面角，
在△C1OC中，C1C=B1B=
，C1O=
，
所以tan∠C1OC=
=
=
，
故答案为：
．
| 3 |
因为C1C⊥底面A1B1C1D1，连接A1C1，交B1D1与O，则C1O⊥B1D1，
连接CO，则∠C1OC即为二面角C-B1D1-C1的平面角，
在△C1OC中，C1C=B1B=
| 3 |
| ||
| 2 |
所以tan∠C1OC=
| C1C |
| C1O |
| ||||
|
| 6 |
故答案为：
| 6 |
练习册系列答案
备战中考寒假系列答案
相关题目
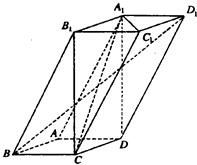如图，四棱柱ABCD-A1B1C1D1中，A1D⊥平面ABCD，底面ABCD是边长为1的正方形，侧棱AA1=2．
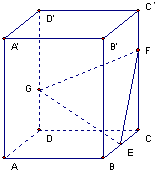如图，正四棱柱ABCD-A′B′C′D′中，底面边长为2，侧棱长为3，E为BC的中点，FG分别为CC′、DD′上的点，且CF=2GD=2．求：
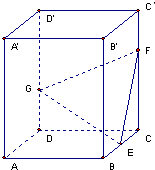如图，正四棱柱ABCD-A′B′C′D′中，底面边长为2，侧棱长为3，E为BC的中点，FG分别为CC′、DD′上的点，且CF=2GD=2．求：