题目内容
F1,F2是椭圆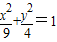 的两个焦点,斜率为1的直线l过左焦点F1,并与椭圆交于A,B两点
的两个焦点,斜率为1的直线l过左焦点F1,并与椭圆交于A,B两点(1)求△ABF2周长.
(2)求△ABF2的面积.
【答案】分析:(1)根据椭圆的定义可得:|AF1|+|AF2|=2a,|BF1|+|BF2|=2a,并且|AF2|+|BF2|=|AB|,进而得到答案.
(2)把直线AB的方程 代入椭圆的方程化简,利用根与系数的关系,求出|AB|的值,利用点到直线的距离,结合三角形的面积公式求得结果.
解答: 解:(1)由椭圆方程可知,a=3,
解:(1)由椭圆方程可知,a=3,
△ABF2周长=AF1+AF2+BF1+BF2=4a=12;
(2)椭圆的左焦点为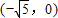 ,所以直线方程为
,所以直线方程为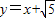 ,
,
联立直线与椭圆方程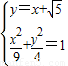 ,消元得
,消元得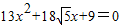 ,
,
则有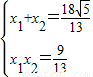 ,
,
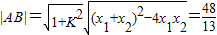 ,
,
点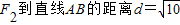 ,
,
所以△ABF2的面积为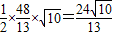 .
.
点评:本题考查椭圆的标准方程,以及椭圆的简单性质的应用,解决此类问题的关键是熟练掌握椭圆的定义.
(2)把直线AB的方程 代入椭圆的方程化简,利用根与系数的关系,求出|AB|的值,利用点到直线的距离,结合三角形的面积公式求得结果.
解答:
 解:(1)由椭圆方程可知,a=3,
解:(1)由椭圆方程可知,a=3,△ABF2周长=AF1+AF2+BF1+BF2=4a=12;
(2)椭圆的左焦点为
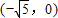 ,所以直线方程为
,所以直线方程为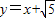 ,
,联立直线与椭圆方程
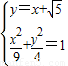 ,消元得
,消元得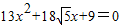 ,
,则有
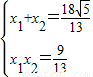 ,
,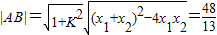 ,
,点
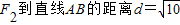 ,
,所以△ABF2的面积为
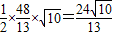 .
.点评:本题考查椭圆的标准方程,以及椭圆的简单性质的应用,解决此类问题的关键是熟练掌握椭圆的定义.

练习册系列答案
相关题目