题目内容
【题目】第三届移动互联创新大赛,于2017年3月~10月期间举行,为了选出优秀选手,某高校先在计算机科学系选出一种子选手![]() ,再从全校征集出3位志愿者分别与
,再从全校征集出3位志愿者分别与![]() 进行一场技术对抗赛,根据以往经验,
进行一场技术对抗赛,根据以往经验, ![]() 与这三位志愿者进行比赛一场获胜的概率分别为
与这三位志愿者进行比赛一场获胜的概率分别为![]() ,且各场输赢互不影响.
,且各场输赢互不影响.
(1)求甲恰好获胜两场的概率;
(2)求甲获胜场数的分布列与数学期望.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:⑴利用相互独立事件的概率计算公式即可得出;
⑵设甲获胜场次为![]() ,则
,则![]() 的可能取值为:
的可能取值为: ![]() ,求出概率,列出分布列,然后求解数学期望
,求出概率,列出分布列,然后求解数学期望
解析:(1)设甲与三位志愿者比赛一场获胜的事件分别为![]() ,
,
则![]() ,
, ![]() ,
, ![]() ,
,
则甲恰好获胜两场的概率为: ![]()
![]()
![]()
![]()
![]() ;
;
(2)设甲获胜场次为![]() ,则
,则![]() 的可能取值为:0,1,2,3,
的可能取值为:0,1,2,3,
则![]()
![]()
![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]() ;
;
![]() ;
;
![]()
![]()
![]() .
.
∴![]() 的分布列为:
的分布列为:

∴![]() 的数学期望为:
的数学期望为:
![]()
![]() .
.

练习册系列答案
相关题目
【题目】某地随着经济的发展,居民收入逐年增长.该地一建设银行统计连续五年的储蓄存款(年底余额)得到下表:
年份 |
|
|
|
|
|
储蓄存款 (千亿元) |
|
|
|
|
|
为便于计算,工作人员将上表的数据进行了处理(令![]() ,
, ![]() ),得到下表:
),得到下表:
时间 |
|
|
|
|
|
储蓄存款 |
|
|
|
|
|
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(Ⅱ)通过(Ⅰ)中的方程,求出![]() 关于
关于![]() 的回归方程;
的回归方程;
(Ⅲ)用所求回归方程预测到![]() 年年底,该地储蓄存款额可达多少?
年年底,该地储蓄存款额可达多少?
附:线性回归方程![]() ,其中
,其中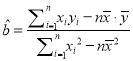 ,
, ![]() .
.
