题目内容
双曲线 的两焦点分别为F1和F2,若双曲线上存在不是顶点的点P,使得∠PF2F1=3∠PF1F2,则双曲线离心率e的取值范围是________.
的两焦点分别为F1和F2,若双曲线上存在不是顶点的点P,使得∠PF2F1=3∠PF1F2,则双曲线离心率e的取值范围是________.
1<e<2
分析:设∠PF1F2=α,在三角形PF1F2中,根据正弦定理,可得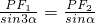 ,利用三倍角公式化简得PF1=(3-4sin2α)PF2,再利用双曲线的定义,可得PF2=
,利用三倍角公式化简得PF1=(3-4sin2α)PF2,再利用双曲线的定义,可得PF2=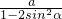 ,最后根据P在双曲线右友,可得关于e的不等式,进而根据三角函数的范围确定e的范围.
,最后根据P在双曲线右友,可得关于e的不等式,进而根据三角函数的范围确定e的范围.
解答:设∠PF1F2=α,
∵∠PF2F1=3∠PF1F2,P在双曲线右支(x>a)
在三角形PF1F2中,根据正弦定理,可得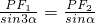 ,
,
即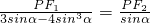
∴PF1=(3-4sin2α)PF2,
∵PF1-PF2=2a,∴(3-4sin2α)PF2-PF2=2a,
∴PF2=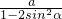 ,
,
由于P在P在双曲线右支,∴PF2>c-a,
∵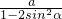 >c-a,∴
>c-a,∴ <1+
<1+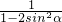 ≤2,
≤2,
∴ <2,又
<2,又 >1,
>1,
则双曲线离心率e的取值范围是 1<e<2.
故答案为:1<e<2.
点评:本题主要考查了双曲线的简单性质,考查了双曲线的第二定义的灵活运用,属于中档题.
分析:设∠PF1F2=α,在三角形PF1F2中,根据正弦定理,可得
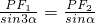 ,利用三倍角公式化简得PF1=(3-4sin2α)PF2,再利用双曲线的定义,可得PF2=
,利用三倍角公式化简得PF1=(3-4sin2α)PF2,再利用双曲线的定义,可得PF2=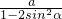 ,最后根据P在双曲线右友,可得关于e的不等式,进而根据三角函数的范围确定e的范围.
,最后根据P在双曲线右友,可得关于e的不等式,进而根据三角函数的范围确定e的范围.解答:设∠PF1F2=α,
∵∠PF2F1=3∠PF1F2,P在双曲线右支(x>a)
在三角形PF1F2中,根据正弦定理,可得
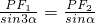 ,
,即
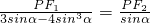
∴PF1=(3-4sin2α)PF2,
∵PF1-PF2=2a,∴(3-4sin2α)PF2-PF2=2a,
∴PF2=
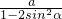 ,
,由于P在P在双曲线右支,∴PF2>c-a,
∵
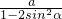 >c-a,∴
>c-a,∴ <1+
<1+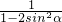 ≤2,
≤2,∴
 <2,又
<2,又 >1,
>1,则双曲线离心率e的取值范围是 1<e<2.
故答案为:1<e<2.
点评:本题主要考查了双曲线的简单性质,考查了双曲线的第二定义的灵活运用,属于中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
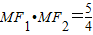 ,
,