题目内容
抛物线y2=2px(p>0)与双曲线x2-y2=1相交的一个交点为M,双曲线的两焦点分别为F1、F2,若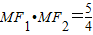 ,
,(I)证明:M点在F1、F2为焦点的椭圆上;
(II)求抛物线方程.
【答案】分析:(I)设M(m,n)(m>0),因M点在双曲线x2-y2=1,根据双曲线的焦半径公式得:MF1=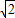 m+1,MF2=
m+1,MF2=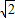 m-1,结合
m-1,结合 求得m的值,从而得出MF1+MF2=3=定值,最后由椭圆的定义得出结论即可;
求得m的值,从而得出MF1+MF2=3=定值,最后由椭圆的定义得出结论即可;
(II)由(I)得M的坐标为:(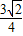 ,
,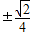 )代入抛物线方程y2=2px(p>0)得焦参数,最后写出抛物线方程.
)代入抛物线方程y2=2px(p>0)得焦参数,最后写出抛物线方程.
解答:解:(I)设M(m,n)(m>0),因M点在双曲线x2-y2=1,
根据双曲线的焦半径公式得:
MF1=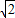 m+1,MF2=
m+1,MF2=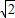 m-1,
m-1,
∵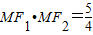
∴(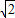 m+1)(
m+1)(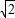 m-1)=
m-1)= ,⇒m=
,⇒m=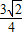
∴MF1+MF2=3=定值,即点M到F1、F2的距离之和为定值,且大于|F1F2|,
由椭圆的定义得:M点在F1、F2为焦点的椭圆上.
(II)由(I)得M的坐标为:(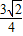 ,
,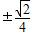 )
)
代入抛物线方程y2=2px(p>0)得:2p=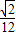
∴抛物线方程是: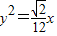 .
.
点评:本小题主要考查圆锥曲线的共同特征、椭圆的方程及几何性质等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.
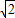 m+1,MF2=
m+1,MF2=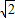 m-1,结合
m-1,结合 求得m的值,从而得出MF1+MF2=3=定值,最后由椭圆的定义得出结论即可;
求得m的值,从而得出MF1+MF2=3=定值,最后由椭圆的定义得出结论即可;(II)由(I)得M的坐标为:(
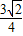 ,
,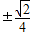 )代入抛物线方程y2=2px(p>0)得焦参数,最后写出抛物线方程.
)代入抛物线方程y2=2px(p>0)得焦参数,最后写出抛物线方程.解答:解:(I)设M(m,n)(m>0),因M点在双曲线x2-y2=1,
根据双曲线的焦半径公式得:
MF1=
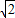 m+1,MF2=
m+1,MF2=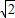 m-1,
m-1,∵
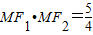
∴(
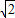 m+1)(
m+1)(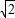 m-1)=
m-1)= ,⇒m=
,⇒m=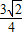
∴MF1+MF2=3=定值,即点M到F1、F2的距离之和为定值,且大于|F1F2|,
由椭圆的定义得:M点在F1、F2为焦点的椭圆上.
(II)由(I)得M的坐标为:(
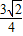 ,
,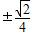 )
)代入抛物线方程y2=2px(p>0)得:2p=
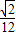
∴抛物线方程是:
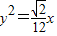 .
.点评:本小题主要考查圆锥曲线的共同特征、椭圆的方程及几何性质等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图过抛物线y2=2px(p>0)的焦点F的直线依次交抛物线及准线于点A,B,C,若|BC|=2|BF|,且|AF|=3,则抛物线的方程为( )
如图过抛物线y2=2px(p>0)的焦点F的直线依次交抛物线及准线于点A,B,C,若|BC|=2|BF|,且|AF|=3,则抛物线的方程为( )A、y2=
| ||
| B、y2=9x | ||
C、y2=
| ||
| D、y2=3x |