题目内容
(本题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分. 第3小题满分8分.
(理)对于数列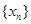 ,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为正整数
,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为正整数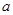 ,公比为正整数
,公比为正整数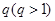 的无穷等比数列
的无穷等比数列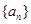 的子数列问题. 为此,他任取了其中三项
的子数列问题. 为此,他任取了其中三项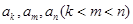 .
.
(1) 若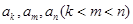 成等比数列,求
成等比数列,求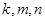 之间满足的等量关系;
之间满足的等量关系;
(2) 他猜想:“在上述数列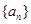 中存在一个子数列
中存在一个子数列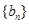 是等差数列”,为此,他研究了
是等差数列”,为此,他研究了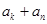 与
与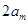 的大小关系,请你根据该同学的研究结果来判断上述猜想是否正确;
的大小关系,请你根据该同学的研究结果来判断上述猜想是否正确;
(3) 他又想:在首项为正整数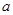 ,公差为正整数
,公差为正整数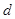 的无穷等差数列中是否存在成等比数列的子数列?请你就此问题写出一个正确命题,并加以证明.
的无穷等差数列中是否存在成等比数列的子数列?请你就此问题写出一个正确命题,并加以证明.
(1)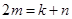 ;(2)不成立;(3) 对于首项为正整数
;(2)不成立;(3) 对于首项为正整数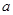 ,公差为正整数
,公差为正整数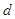 的无穷等差数列
的无穷等差数列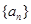 ,总可以找到一个无穷子数列
,总可以找到一个无穷子数列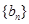 ,使得
,使得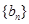 是一个等比数列.
是一个等比数列.
【解析】
试题分析:(1)由已知可得: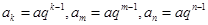 ,
1分
,
1分
则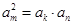 ,即有
,即有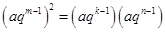 ,
3分
,
3分
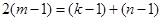 ,化简可得.
,化简可得. 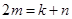 . 4分
. 4分
(2) 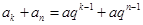 ,又
,又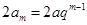 ,
,
故 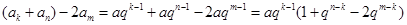 , 6分
, 6分
由于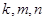 是正整数,且
是正整数,且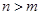 ,则
,则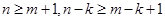 ,
,
又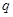 是满足
是满足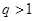 的正整数,则
的正整数,则 ,
,
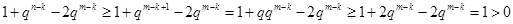 ,
,
所以,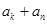 >
>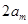 ,从而上述猜想不成立.
10分
,从而上述猜想不成立.
10分
(3)命题:对于首项为正整数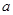 ,公差为正整数
,公差为正整数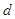 的无穷等差数列
的无穷等差数列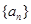 ,总可以找到一个无穷子数列
,总可以找到一个无穷子数列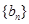 ,使得
,使得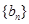 是一个等比数列. 13分
是一个等比数列. 13分
此命题是真命题,下面我们给出证明.
证法一: 只要证明对任意正整数n,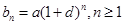 都在数列{an}中.因为bn=a(1+d)n=a(1+
都在数列{an}中.因为bn=a(1+d)n=a(1+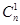 d+
d+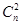 d2+…+
d2+…+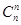 dn)=a(Md+1),这里M=
dn)=a(Md+1),这里M=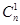 +
+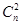 d+…+
d+…+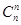 dn-1为正整数,所以a(Md+1)=a+aMd是{an}中的第aM+1项,证毕. 18分
dn-1为正整数,所以a(Md+1)=a+aMd是{an}中的第aM+1项,证毕. 18分
证法二:首项为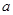 ,公差为
,公差为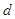 (
( 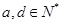 )的等差数列为
)的等差数列为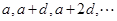 ,考虑数列
,考虑数列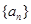 中的项:
中的项: 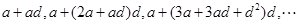
依次取数列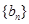 中项
中项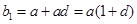 ,
,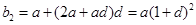 ,
,
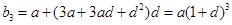 ,则由
,则由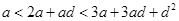 ,可知
,可知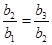 ,并由数学归纳法可知,数列
,并由数学归纳法可知,数列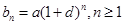 为
为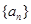 的无穷等比子数列. 18分
的无穷等比子数列. 18分
考点:等比数列的简单性质;数列的综合应用。
点评:此题考查了等差数列的性质即通项公式,同时本题属于新定义及结论探索性问题,这类试题的一般解法是:充分抓住已知条件,找准问题的突破点,由浅入深,多角度、多侧面探寻,联系符合题设的有关知识,合理组合发现新结论,围绕所探究的结论环环相扣,步步逼近发现规律,得出结论.熟练掌握公式及性质是解本题的关键.

 和正数
和正数 ,且对任意的正整数n,当
,且对任意的正整数n,当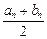 ≥0时, 有[
≥0时, 有[ ,
,  ]=
]= ,
, 
 ].
]. }是等比数列;
}是等比数列; ,求证
,求证
 ;
; ,使得数列
,使得数列 为常数数列?请说明理由
为常数数列?请说明理由 到其准线的距离等于5.
到其准线的距离等于5. 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明 为定值;
为定值; 且
且 与
与 面积之和的最小值.
面积之和的最小值.
 ,对于项数为
,对于项数为 的有穷数列
的有穷数列 ,令
,令 为
为 中最大值,称数列
中最大值,称数列 为
为 3,5,4,7的创新数列为3,5,5,7.
3,5,4,7的创新数列为3,5,5,7. 的所有排列,将每种排列都视为一个有穷数列
的所有排列,将每种排列都视为一个有穷数列 .
. ,写出创新数列为3,4,4,4的所有数列
,写出创新数列为3,4,4,4的所有数列 的首项为1,前
的首项为1,前 项和为
项和为 ,且满足
,且满足 ,
, .数列
.数列 满足
满足 .
.  时,试比较
时,试比较 与
与 的大小,并说明理由;
的大小,并说明理由;
 是否可能恰为直线
是否可能恰为直线
 的方向向量?请说明你的理由.
的方向向量?请说明你的理由.