题目内容
为测河的宽度,在一岸边选定A,B两点,望对岸的标记物C,测得∠CAB=30°,∠CBA=75°,AB=120m.求河的宽度.
考点:解三角形的实际应用
专题:解三角形
分析:根据题意求得∠ACB,确定△ABC为等腰三角形,过C作AB的垂线设交AB于D,求得AD.
解答:
 解:∠ACB=180°-∠CAB-∠CBA=180°-30°-75°=75°
解:∠ACB=180°-∠CAB-∠CBA=180°-30°-75°=75°
所以△ABC为等腰三角形,AC=AB=120(米)
过C作AB的垂线,交AB于D,则
AD=AC•sin30°=120×
=60(米)
即河宽60米
 解:∠ACB=180°-∠CAB-∠CBA=180°-30°-75°=75°
解:∠ACB=180°-∠CAB-∠CBA=180°-30°-75°=75°所以△ABC为等腰三角形,AC=AB=120(米)
过C作AB的垂线,交AB于D,则
AD=AC•sin30°=120×
| 1 |
| 2 |
即河宽60米
点评:本题主要考查了解三角形问题的实际应用.把实际问题转换为三角形的相关问题,是解决问题的关键.

练习册系列答案
相关题目
| ∫ | 1 0 |
| A、e+cos1 |
| B、e-cos1 |
| C、x-sin1 |
| D、e+sin1 |
执行如图的程序框图,输出的T=( )


| A、12 | B、20 | C、42 | D、30 |
sinx=0是cosx=1的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
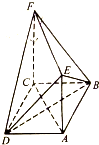 如图,在多面体ABCDEF中,底面ABCD是菱形,AE⊥平面ABCD,CF∥AE,AB=AC=AE=2,EF⊥平面BDE.
如图,在多面体ABCDEF中,底面ABCD是菱形,AE⊥平面ABCD,CF∥AE,AB=AC=AE=2,EF⊥平面BDE.