题目内容
求下列函数的单调区间,并指出其单调性.
(1)y=2x-lnx;
(2)y=![]() +cosx;
+cosx;
(3)y=x3-x.
答案:
解析:
解析:
|
解:(1)函数的定义域为(0,+∞), 其导数为 令2 令2 因此( (2)函数的定义域为R, 令 令 因此f(x)在(2kπ+ (3)函数的定义域为R, 令 令 ∴y=x3-x有三个单调区间,其中在(-∞, 解析:利用导数法求单调区间的方法步骤直接求解. |

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 ; (2)y=
; (2)y= tan2x+1;
tan2x+1;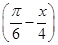 .
.