题目内容
已知函数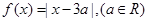
(1)当a=1时,解不等式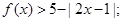
(2)若存在 成立,求a的取值范围.
成立,求a的取值范围.
(1)  (2)
(2)  .
.
解析试题分析:(1)当 时,原不等式等价于
时,原不等式等价于 ,可采用零点分段法解不等式,即分成
,可采用零点分段法解不等式,即分成 ,
, ,
, 三种情况去绝对值,分别解不等式,最后求并集;属于基础题型;
三种情况去绝对值,分别解不等式,最后求并集;属于基础题型;
(2) ,分
,分 和
和 两种情况去绝对值,得到分段函数,得到函数的最小值为
两种情况去绝对值,得到分段函数,得到函数的最小值为 ,若存在
,若存在 成立,只需
成立,只需 的最小值小于6,得到
的最小值小于6,得到 的取值范围,此问属于比较简单的恒成立问题.
的取值范围,此问属于比较简单的恒成立问题.
(1)当 时,不等式
时,不等式
 可化为
可化为 ,
,
当 时,不等式即
时,不等式即
当 时,不等式即
时,不等式即 所以
所以 ,
,
当 时,不等式即
时,不等式即 ,
,
综上所述不等式的解集为 5分
5分
(2)令
所以函数 最小值为
最小值为 ,
,
根据题意可得 ,即
,即 ,所以
,所以 的取值范围为
的取值范围为 . 10分
. 10分
考点:1.解不等式;2.恒成立问题.

练习册系列答案
相关题目

 ;
; 的解集为空集,求实数
的解集为空集,求实数 的取值范围.
的取值范围.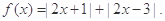
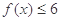 的解集;
的解集;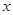 的不等式
的不等式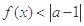 的解集非空,求实数
的解集非空,求实数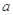 的取值范围.
的取值范围. ,当
,当 时,
时, ;
; 时,
时, 。
。 的解析式
的解析式
 .
. ;
; ,
,  都成立,求实数
都成立,求实数 的取值范围.
的取值范围.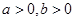 ,且
,且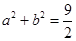 ,若
,若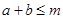 恒成立.
恒成立.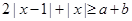 对任意的
对任意的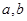 恒成立,求实数x的取值范围.
恒成立,求实数x的取值范围. 时,求不等式f(x)>1的解集.
时,求不等式f(x)>1的解集.