题目内容
已知实数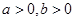 ,且
,且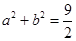 ,若
,若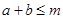 恒成立.
恒成立.
(1)求实数m的最小值;
(2)若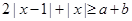 对任意的
对任意的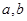 恒成立,求实数x的取值范围.
恒成立,求实数x的取值范围.
(1)3;(2) 或
或 .
.
解析试题分析:本题主要考查基本不等式、恒成立问题、绝对值不等式的解法等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,利用基本不等式先求函数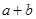 的最大值,再利用恒成立问题得到
的最大值,再利用恒成立问题得到 的最小值为
的最小值为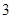 ;第二问,由
;第二问,由 ,先将“
,先将“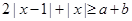 对任意的
对任意的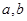 恒成立”转化为“
恒成立”转化为“ ”,利用零点分段法求去掉绝对值,解绝对值不等式,得到x的取值范围.
”,利用零点分段法求去掉绝对值,解绝对值不等式,得到x的取值范围.
(1)
∴ ,∴
,∴
∴ (当且仅当
(当且仅当 时取等号)
时取等号)
又 ,故
,故 ,即
,即 的最小值为
的最小值为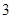 . 5分
. 5分
(2)由(1)
若 对任意的
对任意的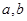 恒成立,故只需
恒成立,故只需
 或
或 或
或
解得 或
或 . 10分
. 10分
考点:基本不等式、恒成立问题、绝对值不等式的解法.

练习册系列答案
相关题目
 的解集是
的解集是 .
. ,求
,求 的取值范围;
的取值范围; ,求不等式
,求不等式 的解集.
的解集.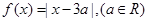
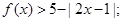
 成立,求a的取值范围.
成立,求a的取值范围. ,求证
,求证 ;
; ,求证:
,求证: .
. 的解集为M,
的解集为M,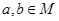 .
.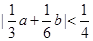 ;
;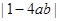 与
与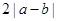 的大小,并说明理由.
的大小,并说明理由.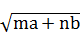 ≥m
≥m +n
+n .
. (n>1,n∈N*)的过程中,用n=k+1时左边的代数式减去n=k时左边的代数式的结果是A,求代数式A.
(n>1,n∈N*)的过程中,用n=k+1时左边的代数式减去n=k时左边的代数式的结果是A,求代数式A.