题目内容
已知
（1）若
，求证
是奇数；
（2）求证对于任意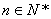
，都存在正整数
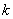，使得
．
（1）由二项式定理得
，
所以
，为奇数．
（2）由（1），设
所以
．
当
为偶数时，
，存在
，使得
；
当为奇数时，
，存在
，使得
；
综上，对于任意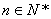，都存在正整数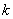，使得．
练习册系列答案
相关题目
题目内容
已知
（1）若，求证是奇数；
（2）求证对于任意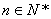，都存在正整数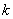，使得．
（1）由二项式定理得，
所以，为奇数．
（2）由（1），设
所以．
当为偶数时，，存在，使得；
当为奇数时，，存在，使得；
综上，对于任意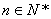，都存在正整数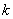，使得．
，则过圆心且与直线l垂直的直线的方程为 ．
轴的正半轴重合.若直线
的极坐标方程为
.
为椭圆
上一点,求
和
，其中
．
，则
的取值范围是 ．
的直径
的延长线与弦
的延长线相交于点
，
为
，求证：
．
，则
的概率为 ．
是定义域为R的奇函数，且x≤0时，
，则函数
的值域为集合A，函数
的定义域为集合B，则A
B = ．