题目内容
函数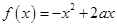 与
与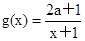 在区间[1,2]上都是减函数,则a的取值范围是
在区间[1,2]上都是减函数,则a的取值范围是
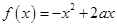 与
与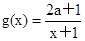 在区间[1,2]上都是减函数,则a的取值范围是
在区间[1,2]上都是减函数,则a的取值范围是A.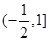 | B. |
C. | D. |
A
试题分析:根据函数
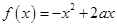 与
与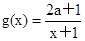 在区间[1,2]上都是减函数,那么可知[1,2]是二次函数减区间的一个子区间,而其开口向下,对称轴为x=a,那么可知
在区间[1,2]上都是减函数,那么可知[1,2]是二次函数减区间的一个子区间,而其开口向下,对称轴为x=a,那么可知 ,而对于
,而对于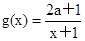 在给定区间是递减,则说明了2a+1>0,a>-
在给定区间是递减,则说明了2a+1>0,a>- ,综上可知,那么参数a的范围是
,综上可知,那么参数a的范围是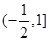 ,选A.
,选A.点评:主要是考查了开口向下的二次函数在对称轴右边为减函数,在对称轴左边为增函数.

练习册系列答案
相关题目
 的图像向左平移
的图像向左平移 个单位,所得曲线的一部分
个单位,所得曲线的一部分 的值分别为
的值分别为




 上的奇函数f(x)在
上的奇函数f(x)在 上是减函数,若f(1-m)< f(m)
上是减函数,若f(1-m)< f(m) 的取值范围.
的取值范围.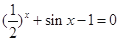 ,下列命题中:①该方程没有小于0的实数解;②该方程有无数个实数解;③该方程在(–∞,0)内有且只有一个实数解;④若
,下列命题中:①该方程没有小于0的实数解;②该方程有无数个实数解;③该方程在(–∞,0)内有且只有一个实数解;④若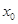 是该方程的实数解,则
是该方程的实数解,则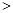 –1.则正确命题是 .
–1.则正确命题是 . 的图象恰好有3个不同的公共点,则实数m的取值范围是( )
的图象恰好有3个不同的公共点,则实数m的取值范围是( )



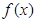 ,对任意x1,x2∈[0,+∞),(x1≠x2),有
,对任意x1,x2∈[0,+∞),(x1≠x2),有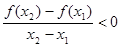 ,
, 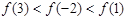
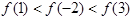
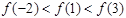
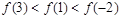
 的定义域为
的定义域为 ,则
,则 的定义域为 .
的定义域为 .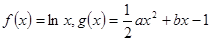 ,
,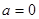 且
且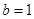 时,证明:对
时,证明:对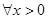 ,
,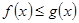 ;
;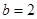 ,且
,且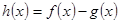 存在单调递减区间,求
存在单调递减区间,求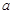 的取值范围;
的取值范围;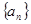 ,若存在常数
,若存在常数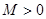 ,
,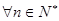 ,都有
,都有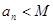 ,则称数列
,则称数列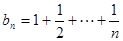 ,试判断数列
,试判断数列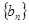 是否有上界.
是否有上界. 的图像如图所示,
的图像如图所示, 为
为 的导函数,则
的导函数,则 ,
, 的大小关系是()
的大小关系是()



