Question

13．设∅（x-1）=$\left\{\begin{array}{l}{1，x≥1}\\{-1，x＜1}\end{array}\right.$，求y=∅（x）的表达式并画出y=∅（x）的图象．

Answer 1

分析 根据函数图象的平移即可得到函数的解析式，画出图象即可．

解答 解：∵∅（x-1）=$\left\{\begin{array}{l}{1，x≥1}\\{-1，x＜1}\end{array}\right.$，
∴∅（x）=$\left\{\begin{array}{l}{1，x≥0}\\{-1，x＜0}\end{array}\right.$，
其图象为：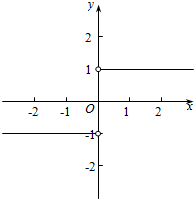

点评 本题考查了函数图象的平移以及函数解析式的求法和函数图象的画法，属于基础题．