题目内容
若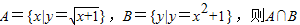 = .
= .
【答案】分析:分别解出集合A和B,然后根据集合交集的定义进行求解;
解答:解:∵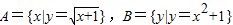 ,
,
可支集合A中的元素是x,集合B中的元素是y,
∴x+1≥0,y=x2+1≥1,
∴A={x|x≥-1},B={y|y≥1},
∴A∩B=[1,+∞),
故答案为[1,+∞).
点评:此题主要考查集合交集及其运算,解题时注意A,B,中的代表元素是什么,许多同学会出错,解出A={x|x≥0},这一点同学们要注意;
解答:解:∵
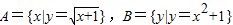 ,
,可支集合A中的元素是x,集合B中的元素是y,
∴x+1≥0,y=x2+1≥1,
∴A={x|x≥-1},B={y|y≥1},
∴A∩B=[1,+∞),
故答案为[1,+∞).
点评:此题主要考查集合交集及其运算,解题时注意A,B,中的代表元素是什么,许多同学会出错,解出A={x|x≥0},这一点同学们要注意;

练习册系列答案
相关题目
若双曲线
-
=1(a>b>0)的左右焦点分别为F1、F2,线段F1F2被抛物线y2=2bx的焦点分成7:5的两段,则此双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|