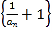题目内容
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() .
.
(1)若函数![]() 的图象均在
的图象均在![]() 轴上方,求
轴上方,求![]() 的取值范围;
的取值范围;
(2)记![]() 为函数
为函数![]() 在
在![]() 上的零点,若存在唯一的
上的零点,若存在唯一的![]() ,使得
,使得![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)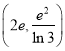 .
.
【解析】
(1)由题意可知,不等式![]() 对任意的
对任意的![]() 恒成立,利用导数求出函数
恒成立,利用导数求出函数![]() 的最小值,可得出关于实数
的最小值,可得出关于实数![]() 的不等式,即可求得实数
的不等式,即可求得实数![]() 的取值范围;
的取值范围;
(2)先利用“![]() 为函数
为函数![]() 在
在![]() 上的零点”得到
上的零点”得到![]() 的取值范围,并得到结论
的取值范围,并得到结论![]() ,然后利用另一个条件,再次得到
,然后利用另一个条件,再次得到![]() 的取值范围,其中涉及隐零点问题,最后综合两次所得
的取值范围,其中涉及隐零点问题,最后综合两次所得![]() 的取值范围求出结果.
的取值范围求出结果.
(1)由题意可得不等式![]() 对任意的
对任意的![]() 恒成立,则
恒成立,则![]() ,
,
![]() ,则
,则![]() ,令
,令![]() ,列表如下:
,列表如下:
|
|
|
|
|
|
|
|
|
| 极小值 |
|
所以,函数![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() .
.
所以,函数![]() 的最小值为
的最小值为![]() ,
,
由题意可得![]() ,解得
,解得![]() ,
,
因此,实数![]() 的取值范围是
的取值范围是![]() ;
;
(2)由(1)可知,函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
因为![]() 为函数
为函数![]() 在
在![]() 上的零点,所以,
上的零点,所以,![]() ,①
,①
且有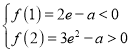 ,解得
,解得![]() .
.
![]() ,
,![]() ,
,
令![]() ,则
,则![]() ,
,
![]() ,
,![]() ,函数
,函数![]() 单调递增,即函数
单调递增,即函数![]() 单调递增,
单调递增,
而![]() ,
,![]() ,
,
所以,存在![]() ,使得
,使得![]() ,即
,即![]() ,②
,②
当![]() 时,
时,![]() ,此时,函数
,此时,函数![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,此时,函数
,此时,函数![]() 单调递增.
单调递增.
所以,函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,
,
由①②得![]() ,所以,
,所以,![]() ,
,
所以,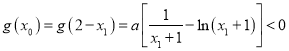 在
在![]() 上恒成立,
上恒成立,
又因为存在唯一的![]() ,使得
,使得![]() 且
且![]() ,则
,则![]() ,
,
所以![]() ,
,![]() ,解得
,解得![]() .
.
![]() ,
,![]() ,因此,实数
,因此,实数![]() 的取值范围是
的取值范围是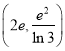 .
.

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案【题目】世界读书日又称“世界图书日”,设立的目的是希望世界各地的人,无论你是年老还是年轻,都能享受阅读的乐趣,都能尊重和感谢为人类文明做出巨大贡献的文学、文化、科学、思想大师们,都能保护知识产权.某单位共有600人,其年龄与人数分布表如下:
年龄段 |
|
|
|
|
人数(单位:人) | 150 | 210 | 180 | 60 |
约定:年龄在![]() 为青年人,在
为青年人,在![]() 为中老年人.今年年初,该单位开展“每天阅读1小时”活动,为了了解员工阅读1小时是否与年龄相关,一个月后按照分层抽样抽取30人进行调查.
为中老年人.今年年初,该单位开展“每天阅读1小时”活动,为了了解员工阅读1小时是否与年龄相关,一个月后按照分层抽样抽取30人进行调查.
(1)抽出的青年人与中老年人数量分别为多少?并估算单位这600人的平均年龄;
(2)若所抽取出的青年人与中老年人中分别有6人和7人平均每天阅读达1小时,其余人都没达1小时.完成下列2×2列联表,并回答能否由90%的把握认为年龄与阅读达1小时有关?
阅读达1小时 | 阅读没达1小时 | 总计 | |
青年 | 6 | ||
中年 | 7 | ||
总计 | 30 |
参考公式: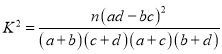
临界值表:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |