题目内容
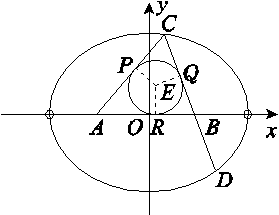
已知△ABC的两顶点坐标A(-1,0),B(1,0),圆E是△ABC的内切圆,在边AC,BC,AB上的切点分别为P,Q,R,|CP|=1(从圆外一点到圆的两条切线长相等),动点C的轨迹为曲线M.
(1)求曲线M的方程;
(2)设直线BC与曲线M的另一交点为D,当点A在以线段CD为直径的圆上时,求直线BC的方程.
解:(1)由题知,|CA|+|CB|=|CP|+|CQ|+|AP|+|BQ|=2|CP|+|AB|=4>|AB|,∴曲线M是以A,B为焦点,长轴长为4的椭圆(除去与x轴的交点).
设曲线M: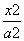 +
+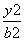 =1(a>0>0,y≠0),则2a=4,2c=2,∴a=2,c=1,b2=a2-c2=3.
=1(a>0>0,y≠0),则2a=4,2c=2,∴a=2,c=1,b2=a2-c2=3.
∴曲线M: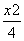 +
+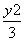 =1(y≠0).
=1(y≠0).
(2)注意到直线BC的斜率不为0,且过定点B(1,0),
设直线BC:x=my+1,C(x1,y1),D(x2,y2).
由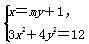 消去x,得
消去x,得
(3m2+4)y2+6my-9=0.
Δ=36m2+36(3m2+4)>0.
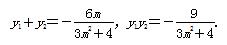 ∵
∵ =(my1+2,y1),
=(my1+2,y1),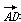 =(my2+2,y2),
=(my2+2,y2),
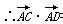 =(my1+2)(my2+2)+y1y2
=(my1+2)(my2+2)+y1y2
=(m2+1)y1y2+2m(y1+y2)+4
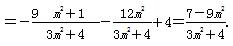 ∵点A在以CD为直径的圆上,
∵点A在以CD为直径的圆上,
∴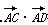 =0,∴m=±
=0,∴m=± .
.
∴直线BC的方程为3x+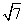 y-3=0或3x-
y-3=0或3x-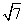 y-3=0.
y-3=0.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目

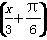 ,f(3α+π)=
,f(3α+π)= ,f
,f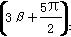 =-
=-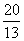 ,其中α,β∈
,其中α,β∈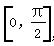 ,则cos(α-β)的值为( )
,则cos(α-β)的值为( )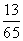 B.
B.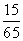 C.
C.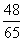 D.
D.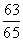
 B. 16
B. 16 C. 9
C. 9
 与时间
与时间 (月)的关系:
(月)的关系: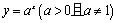 ,有以下叙述:
,有以下叙述: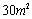 ;
;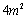 蔓延到
蔓延到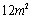 需要经过
需要经过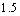 个月;
个月;