题目内容
【题目】已知椭圆![]() 的标准方程为
的标准方程为![]() ,该椭圆经过点
,该椭圆经过点![]() ,且离心率为
,且离心率为![]() .
.
(1)求椭圆的标准方程;
(2)过椭圆![]() 长轴上一点
长轴上一点![]() 作两条互相垂直的弦
作两条互相垂直的弦![]() .若弦
.若弦![]() 的中点分别为
的中点分别为![]() ,证明:直线
,证明:直线![]() 恒过定点.
恒过定点.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据已知得到方程组,解方程组即得椭圆的方程.(2)先求直线MN的方程![]() ,
,![]() ,即得直线MN经过的定点,再讨论当
,即得直线MN经过的定点,再讨论当![]() 时,直线
时,直线![]() 也经过定点
也经过定点![]() ,综上所述,直线
,综上所述,直线![]() 经过定点
经过定点![]() .当
.当![]() 时,过定点
时,过定点![]() .
.
(1)解:∵点![]() 在椭圆上,∴
在椭圆上,∴![]() ,
,
又∵离心率为![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,解得
,解得![]() ,
,![]() ,
,
∴椭圆方程为![]() .
.
(2)证明:设直线![]() 的方程为
的方程为![]() ,
,![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,
,
联立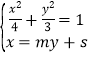 ,得
,得![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
∴![]() ,
,
由中点坐标公式得![]() ,
,
将![]() 的坐标中的
的坐标中的![]() 用
用![]() 代换,得
代换,得![]() 的中点
的中点![]() ,
,
∴直线![]() 的方程为
的方程为![]() ,
,![]() ,
,
令![]() 得
得![]() ,∴直线
,∴直线![]() 经过定点
经过定点![]() ,
,
当![]() 时,直线
时,直线![]() 也经过定点
也经过定点![]() ,综上所述,直线
,综上所述,直线![]() 经过定点
经过定点![]() .
.
当![]() 时,过定点
时,过定点![]() .
.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
【题目】为了选拔参加自行车比赛的选手,对自行车运动员甲、乙两人在相同条件下进行了6次测试,测得他们的最大速度(单位:m/s)的数据如下:
甲 | 27 | 38 | 30 | 37 | 35 | 31 |
乙 | 33 | 29 | 38 | 34 | 28 | 36 |
(1)画出茎叶图,由茎叶图你能获得哪些信息;
(2)估计甲、乙两运动员的最大速度的平均数和方差,并判断谁参加比赛更合适.