题目内容

已知数列{an}满足：a1为正整数，an+1=
an
2
，an为偶数
3an+1，an为奇数
，如果a1=1，则a1+a2+…+a2004=
 
．
考点：数列的概念及简单表示法
专题：等差数列与等比数列
分析：由an+1=
an
2
，an为偶数
3an+1，an为奇数
，a1=1，可得a2=4，a3=2，a4=1．…可得an+3=an．即可得出．
解答： 解：由an+1=
an
2
，an为偶数
3an+1，an为奇数
，a1=1，可得a2=3a1+1=4，a3=
a2
2
=2，a4=
a3
2
=1．
∴可得an+3=an．
∴a1+a2+…+a2004=668（a1+a2+a3）=668×7=4676．
故答案为：4676．
点评：本题考查了分段函数的意义、数列的周期性，考查了推理能力和计算能力，属于中档题．
练习册系列答案
相关题目
交通银行向市场推出甲、乙两种理财产品，若投资甲、乙两种理财产品分别为p，q万元，到期后获得的收益分别为
1
10
p，
2
5
lnq万元，且要求每种产品的投资起点都不低于1万元．现在张老师把10万元全部用于投资这两种理财产品．
（Ⅰ）若张老师投资了乙种理财产品为8万元，求到期后张老师获得的总收益；
（Ⅱ）请你设计一个投资方案，使得到期后张老师获得的总收益最大，并求出其最大总收益．（参考数据：ln2≈0.7）
已知函数f（x）=
1
x-m
，若存在α∈（0，
π
2
），使f（sinα）+f（cosα）=0，则实数m的取值范围是
 
．
若f（x）=log3（x-1）（x＞1），则f′（2）=
 
．
十二届全国人大二次会议上，李克强总理提出“以雾霾频发的特大城市和区域为重点，以细颗粒物PM2.5和可吸入颗粒物PM10为突破口…”治理污染，“要像对贫困宣战一样，坚决向污染宣战”，其中总理提到的“PM2.5”是指大气中直径小于或等于2.5微米的颗粒物，也称为人肺颗粒物．根据现行国家标准GB3095-2012，PM2.5日均值在35微克/立方米-75微克/立方米之间空气质量为二级；在75微克/立方米以上空气质量为超标．从某市2013年全年每天的PM2.5监测值数据中随机地抽取12天的数据作为样本，监测值频数如茎叶图所示（十位为茎，个位为叶）：
（1）求空气质量为超标的数据的平均数与方差；
（2）在空气质量为二级的数据中任取2个，求这2个数据的和小于100的概率；
（3）以这12天的PM2.5日均值来估计2013年的空气质量状况，则2013年（按366天算）中平均有多少天的空气质量达到一级或二级．
阅读程序框图，运行相应的程序，当输入x的值为-100时，输出x的值为
 
．
已知m，n是不重合的两条直线，α，β是不重合的两个平面．下列命题：
①若α⊥β，m⊥α，则m∥β；       ②若m⊥α，m⊥β，则α∥β；
③若m∥α，m⊥n，则n⊥α；       ④若m∥α，m?β，则α∥β．
其中所有真命题的序号是
 
．
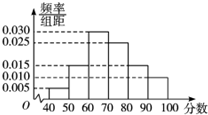某校从高一年级学生中随机抽取部分学生，将他们的模块测试成绩分为6组：[40，50），[50，60），[60，70），[70，80），[80，90），[90，100）加以统计，得到如图所示的频率分布直方图，已知高一年级共有600名，据此估计，该模块测试成绩的平均分为
 
分．
若（x-
1
x
）n展开式的二项式系数之和为64，则展开式的常数项为（　　）
A、10B、-20
C、20D、-120

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网