题目内容
18.中心在原点,对称轴是坐标轴,且过点(0,2)的等轴双曲线的方程为y2-x2=4.分析 设等轴双曲线的方程为x2-y2=λ≠0.把点P(0,2)代入解得λ即可.
解答 解:设等轴双曲线的方程为x2-y2=λ≠0.
把点(0,2)代入可得:-4=λ,即λ=-4.
∴要求的等轴双曲线的方程为y2-x2=4.
故答案为:y2-x2=4.
点评 本题考查双曲线的简单性质的应用,熟练掌握等轴双曲线的标准方程是解题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
9.若α为第三象限角,则$\sqrt{1-sin{α}^{2}}$的结果为( )
| A. | sinα | B. | -sinα | C. | cosα | D. | -cosα |
13.公比为2的正项等比数列{an},a3a11=16,则a5=( )
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
10.直线x-$\sqrt{3}$y+3=0的斜率是( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | -$\frac{{\sqrt{3}}}{3}$ | D. | -$\sqrt{3}$ |
8.如图所示,程序据图(算法流程图)的输出结果为( )
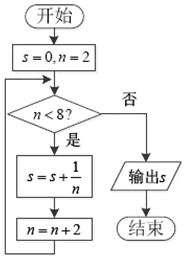

| A. | $\frac{3}{4}$ | B. | $\frac{1}{6}$ | C. | $\frac{11}{12}$ | D. | $\frac{25}{24}$ |
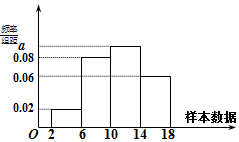 如图是容量为100的样本的频率分布直方图,其中a∈R.试根据图中的数据回答下列问题:
如图是容量为100的样本的频率分布直方图,其中a∈R.试根据图中的数据回答下列问题: