题目内容
18.等差数列-1,4,…的前10项之和为215.分析 由已知等差数列得到首项和公差,然后代入等差数列的前n项和公式得答案.
解答 解:∵等差数列-1,4,…的首项为-1,公差为5,
∴${S}_{10}=10×(-1)+\frac{10×9}{2}×5=215$.
故答案为:215.
点评 本题考查等差数列的前n项和,是基础的计算题.

练习册系列答案
相关题目
6.若实数a,b在区间[0,$\sqrt{2}$]上取值,则函数f(x)=$\frac{2}{3}$ax3+bx2+ax在R上有两个相异极值点的概率是( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{\sqrt{2}}{8}$ | D. | $\frac{1}{2}$ |
13.一几何体的三视图如图所示,则该几何体的表面积为( )
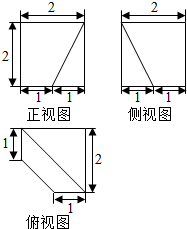

| A. | 20 | B. | 24 | C. | 16 | D. | $16+\frac{3}{2}\sqrt{10}$ |
3.用数学归纳法证明不等式$\frac{n+2}{2}$<1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+…+$\frac{1}{{2}^{n}}$<n+1(n>1,n∈N*)的过程中,当n=2时,中间式子为( )
| A. | 1 | B. | 1+$\frac{1}{2}$ | C. | 1+$\frac{1}{2}$+$\frac{1}{3}$ | D. | 1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$ |
8.cos(-570°)的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |