题目内容
10.已知f(x)=$\frac{ax+b}{1+{x}^{2}}$(a,b为常数)是定义在(-1,1)上的奇函数,且f($\frac{1}{2}$)=$\frac{4}{5}$.(1)求函数f(x)的解析式;
(2)用定义证明f(x)在(-1,1)上是增函数.
分析 (1)根据函数f(x)是定义在(-1,1)上的奇函数,可得f(0)=0,结合f($\frac{1}{2}$)=$\frac{4}{5}$,可求出a,b值,进而得到函数f(x)的解析式;
(2)直接利用函数单调性的定义进行证明,设在(-1,1)上任取两个数x1,x2,且x1<x2,然后判定f(x1)-f(x2)的符号,从而得到结论.
解答 解:(1)∵f(x)=$\frac{ax+b}{1+{x}^{2}}$(a,b为常数)是定义在(-1,1)上的奇函数,
且f($\frac{1}{2}$)=$\frac{4}{5}$,
∴f($\frac{1}{2}$)=$\frac{\frac{1}{2}a+b}{1+\frac{1}{4}}$=$\frac{4}{5}$,即$\frac{1}{2}$a+b=1,①,
f(-$\frac{1}{2}$)=$\frac{-\frac{1}{2}a+b}{1+\frac{1}{4}}$=-$\frac{4}{5}$,即-$\frac{1}{2}$a+b=-1,②,
由①②解得:a=2,b=0,
故f(x)=$\frac{2x}{1{+x}^{2}}$;
(2)任取任取两个数x1,x2∈(-1,1),且x1<x2,
则f(x1)-f(x2)=$\frac{{2x}_{1}}{1{{+x}_{1}}^{2}}$-$\frac{{2x}_{2}}{1{{+x}_{2}}^{2}}$=$\frac{2{(x}_{1}{-x}_{2})(1{-x}_{1}{•x}_{2})}{(1{{+x}_{1}}^{2})(1{{+x}_{2}}^{2})}$<0
因为x1,x2∈(-1,1),且x1<x2,
∴x1-x2<0,1+x12>0,1+x22>0,1-x1•x2>0
则f(x1)<f(x2)
故函数f(x)在(-1,1)上单调递增.
点评 本题主要考查了函数奇偶性的性质,函数单调性的证明,解题的关键是化简判定符号,同时考查了运算求解的能力.

 53随堂测系列答案
53随堂测系列答案| A. | 13 | B. | 8 | C. | 21 | D. | 10 |
 (理科)如图,已知四棱锥P-ABCD的底面ABCD为菱形,且∠ABC=60°,AB=PC=2,PA=PB=$\sqrt{2}$,
(理科)如图,已知四棱锥P-ABCD的底面ABCD为菱形,且∠ABC=60°,AB=PC=2,PA=PB=$\sqrt{2}$,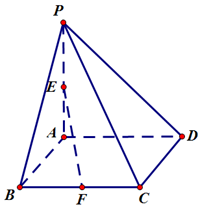 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为矩形,F是BC的中点,且PA=BC=2AB=2.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为矩形,F是BC的中点,且PA=BC=2AB=2.