题目内容
13.已知曲线C的参数方程为$\left\{\begin{array}{l}x=2+cosθ\\ y=1+sinθ\end{array}\right.$(θ∈[0,π]),且点P(x,y)在曲线C上,则$\frac{y-1}{x}$的取值范围是( )| A. | $[{0,\frac{{\sqrt{3}}}{3}}]$ | B. | $[{0,\frac{{\sqrt{3}}}{2}}]$ | C. | $[{1,\frac{{\sqrt{3}}}{3}}]$ | D. | $[{0,\sqrt{3}}]$ |
分析 将曲线C的参数方程化为普通方程,由参数的范围画出图象,由直线的斜率公式求出式子$\frac{y-1}{x}$的几何意义,利用切线的条件、点到直线的距离公式列出方程求解后,结合图象求出答案.
解答 解:因为曲线C的参数方程为$\left\{\begin{array}{l}x=2+cosθ\\ y=1+sinθ\end{array}\right.$(θ∈[0,π]),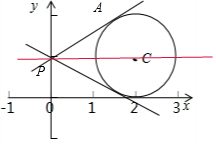
所以曲线C的普通方程是(x-2)2+(y-1)2=1(y≥1),
如图所示:圆C只取直线PC:y=1的上方,
式子$\frac{y-1}{x}$的几何意义是:圆C上的点与定点(0,1)连线的斜率,
所以式子的取值范围处在直线PC与切线PA之间,
设$\frac{y-1}{x}=k$,则kx-y+1=0,又圆心C(2,1),
所以$\frac{|2k-1+1|}{\sqrt{{k}^{2}+1}}=1$,解得k=$±\frac{\sqrt{3}}{3}$,
则$\frac{y-1}{x}$的取值范围是[0,$\frac{\sqrt{3}}{3}$],
故选A.
点评 本题考查参数方程与普通方程互化,直线的斜率公式,以及点到直线的距离公式,考查数形结合思想,化简、变形能力.

练习册系列答案
相关题目
4.已知函数f(x)=x(x-m)2在x=2处取得极小值,则常数m的值为( )
| A. | 2 | B. | 6 | C. | 2或6 | D. | 以上答案都不对 |
 在平面直角坐标系xOy中,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$的右焦点为$(\sqrt{2},0)$,且经过点$(\frac{{\sqrt{2}}}{2},-\frac{{\sqrt{7}}}{2})$,过椭圆的左顶点A作直线l⊥x轴,点M为直线l上的动点(点M与点A不重合),点B为椭圆右顶点,直线BM交椭圆C于点P.
在平面直角坐标系xOy中,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$的右焦点为$(\sqrt{2},0)$,且经过点$(\frac{{\sqrt{2}}}{2},-\frac{{\sqrt{7}}}{2})$,过椭圆的左顶点A作直线l⊥x轴,点M为直线l上的动点(点M与点A不重合),点B为椭圆右顶点,直线BM交椭圆C于点P.