题目内容
16.已知F1(-1,0),F2(1,0),且△PF1F2的周长为6.(Ⅰ)求动点P轨迹C的方程;
(Ⅱ)若不过原点的直线l:y=kx+m与曲线C交于两个不同的点A、B,M为AB的中点,且M到F2的距离等于到直线x=-1的距离,求直线l斜率的取值范围.
分析 (Ⅰ)由F1(-1,0),F2(1,0),则|F1F2|=2,则|PF1|+|PF2|=4>|F1F2|=2,点P轨迹为以F1,F2为焦点的椭圆(不包括左右顶点),设椭圆的标准方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(y≠0)$,由a=2,c=1,b2=a2-c2=4-1=3,即可求得动点P轨迹C的方程;
(Ⅱ)当k=0显然不符合题意,当k≠0时,设直线l:y=kx+m,代入椭圆方程,△>0,整理得4k2-m2+3>0,由韦达定理可知${x_1}+{x_2}=-\frac{8km}{{4{k^2}+3}}=2{x_0}$,即可求得y0=$\frac{3m}{4{k}^{2}+3}$,由M(x0,y0)在抛物线E:y2=4x上,由$m≠0∴m=-\frac{16}{9}{k^2}(4{k^2}+3)$,代入可知256k2(4k2+3)<81,即可求得k的取值范围.
解答 解:(Ⅰ)由F1(-1,0),F2(1,0),则|F1F2|=2,
△PF1F2的周长为6,则|PF1|+|PF2|=4>|F1F2|=2,
∴点P轨迹为以F1,F2为焦点的椭圆(不包括左右顶点),
设椭圆的标准方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(y≠0)$,
∵2a=4,2c=2,即a=2,c=1,
由b2=a2-c2=4-1=3,
∴轨迹C的方程为:$\frac{x^2}{4}+\frac{y^2}{3}=1(y≠0)$;…(6分)
(Ⅱ)当k=0显然不符合题意 …(7分)
当k≠0时,设A(x1,y1),B(x2,y2),AB中点为M(x0,y0),设直线l:y=kx+m,
∴$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1(y≠0)}\end{array}\right.$,整理得:(4k2+3)x2+8kmx+4m2-12=0,
由△>0,整理得4k2-m2+3>0…(1)式 …(10分)
由韦达定理得:${x_1}+{x_2}=-\frac{8km}{{4{k^2}+3}}=2{x_0}$,
∴${x_0}=-\frac{4km}{{4{k^2}+3}}$,代入y=kx+m,则y0=$\frac{3m}{4{k}^{2}+3}$,
由条件可知M(x0,y0)在抛物线E:y2=4x上,
代入M点坐标
∵$m≠0∴m=-\frac{16}{9}{k^2}(4{k^2}+3)$…(2)式…(12分)
将(2)式代入(1)式得:256k2(4k2+3)<81,解得k2<$\frac{3}{32}$,
即-$\frac{\sqrt{6}}{8}$<k<$\frac{\sqrt{6}}{8}$,…(14分)
综上所述,k的取值范围为(-$\frac{\sqrt{6}}{8}$,0)∪(0,$\frac{\sqrt{6}}{8}$).…(15分)
点评 本题考查椭圆的标准方程,考查点的轨迹方程的求法,考查直线与椭圆的位置关系,韦达定理,中点坐标公式,考查计算能力,属于中档题.

| A. | p(n)对所有正整数n都成立 | B. | p(n)对所有正偶数n都成立 | ||
| C. | p(n)对大于或等于2的正整数n都成立 | D. | p(n)对所有自然数都成立 |
 某3D打印机,其打出的产品质量按照百分制衡量,若得分不低于85分则为合格品,低于85分则为不合格品,商家用该打印机随机打印了15件产品,得分情况如图;
某3D打印机,其打出的产品质量按照百分制衡量,若得分不低于85分则为合格品,低于85分则为不合格品,商家用该打印机随机打印了15件产品,得分情况如图;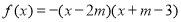 (其中
(其中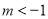 ),
),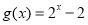 .
.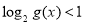 ”是真命题,求
”是真命题,求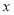 的取值范围;
的取值范围;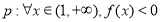 或
或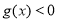 ;命题
;命题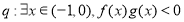 ,若
,若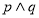 是真命题,求
是真命题,求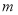 的取值范围.
的取值范围. ,圆
,圆 :
: ,过点
,过点 的动直线
的动直线 与圆
与圆 相交于
相交于 、
、 两点,线段
两点,线段 的中点为
的中点为 ,且
,且 在圆
在圆 上.
上. (
( )经过点
)经过点 ,求
,求 的最大值;
的最大值; 的方程;
的方程; 的直线
的直线 与圆
与圆 相交于
相交于 ,
, 两点,线段
两点,线段 的中点为
的中点为 .
. 与
与 :
: 的交点为
的交点为 ,求证:
,求证: 为定值.
为定值.