题目内容
(本题满分12分)三棱锥 中,
中, ,
, ,
, .
. 
(Ⅰ)求证:平面 平面
平面 ;
;
(Ⅱ)若 ,且异面直线
,且异面直线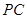 与
与 的夹角为
的夹角为 时,求二面角
时,求二面角 的余弦值.
的余弦值.
(1)通过建立空间直角坐标系来分析,或者利用线面垂直 平面
平面 ,进而得到面面垂直。
,进而得到面面垂直。
(2)
解析试题分析:证明:(Ⅰ)作 平面
平面 于点
于点 ,∵
,∵ ,
,
∴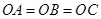 ,即
,即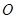 为
为 的外心
的外心
又∵ 中,
中,
故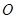 为
为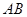 边的中点
边的中点
所以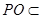 平面
平面
即证:平面 平面
平面 . .......6分
. .......6分
(Ⅱ)∵ 中,
中, ,
, ,∴
,∴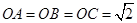
∵ ,且异面直线
,且异面直线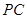 与
与 的夹角为
的夹角为 ,
,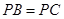
∴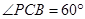 ,∴
,∴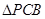 为正三角形,可解得
为正三角形,可解得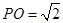 .
.
以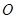 为坐标原点,建立如图所示空间直角坐标系
为坐标原点,建立如图所示空间直角坐标系 ,则
,则 ,
,  ,
,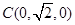 ,
,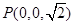
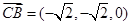
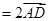 ,∴
,∴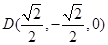 . …………………….9分
. …………………….9分
设平面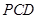 的法向量为
的法向量为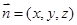
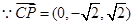 ,
,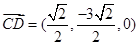
由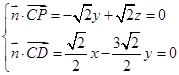 , 取
, 取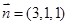
平面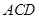 的法向量为
的法向量为
∴ .
.
由图可知,所求二面角 为钝角,其的余弦值为
为钝角,其的余弦值为 . ……….12分
. ……….12分
考点:本试题主要是考查了线线垂直的证明,以及二面角的求解知识。
点评:解决该类立体几何问题,尤其是二面角的求解,通常情况下,都是建立空间直角坐标系,借助于法向量来求解二面角的方法。而对于面面垂直的证明,一般都是利用线面垂直为前提,结合面面垂直的判定定理得到,属于中档题。

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
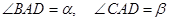 ,
,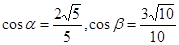 .
.
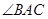 的大小;
的大小;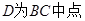 时,判断
时,判断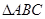 的形状,并求
的形状,并求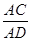 的值.
的值. 的底面
的底面 为菱 形 ,AC∩BD=O侧棱
为菱 形 ,AC∩BD=O侧棱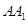 ⊥BD,点F为
⊥BD,点F为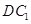 的中点.
的中点.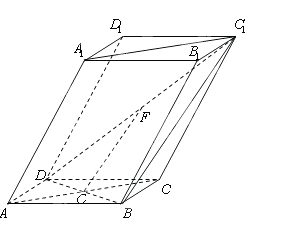
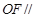 平面
平面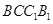 ;
;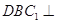 平面
平面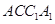 .
. 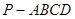 中,底面ABCD是边长为a的正方形,侧面
中,底面ABCD是边长为a的正方形,侧面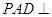 底面ABCD,且
底面ABCD,且 ,若E,F分别为PC,BD的中点.
,若E,F分别为PC,BD的中点.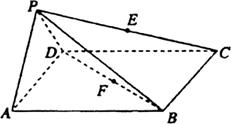
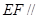 平面PAD;
平面PAD;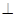 平面PAD;
平面PAD; 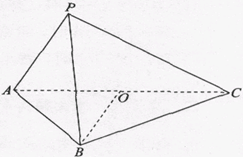
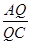 的值;若不存在,说明理由。
的值;若不存在,说明理由。 BCD=60
BCD=60 ,E是CD的中点,PA
,E是CD的中点,PA 底面ABCD,PA=2.
底面ABCD,PA=2.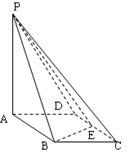
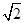 ,∠ABD=90°,E是BD上的一个动点,现将该平行四边形沿对角线BD折成直二面角A-BD-C,如图2所示.
,∠ABD=90°,E是BD上的一个动点,现将该平行四边形沿对角线BD折成直二面角A-BD-C,如图2所示.
 是正三角形,
是正三角形,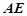 和
和 都垂直于平面
都垂直于平面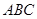 ,且
,且 ,
,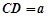 ,
,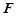 是
是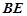 的中点.
的中点.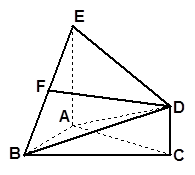
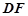 ∥平面
∥平面 的体积.
的体积.