题目内容
10．若一个三位正整数的十位数字比个位数字和百位数字都大，则称这个数为“伞数”，现从1，2，3，4，5这5个数字中任取3个数字，组成没有重复数字的三位数，其中“伞数”共有20个．分析 根据题意，因十位上的数最大，则其只能为3、4、5，进而分3种情形处理，即当十位数字分别为3、4、5时，计算每种情况下百位、个位的数字的情况数目，由分类计数原理，计算可得答案．
解答 解：根据题意，十位上的数最大，只能为3、4、5，
分3种情形处理，当十位数字为3时，百位、个位的数字为1、2，有A22种选法，
当十位数字为4时，百位、个位的数字为1、2、3，有A32种选法，
当十位数字为5时，百位、个位的数字为1、2、3、4，有A42种选法，
则伞数的个数为A22+A32+A42=20；
故答案为：20．
点评 本题考查排列、组合的运用；分析题意是要注意到十位数字特殊，要对其进行分类讨论．
练习册系列答案
手拉手全优练考卷系列答案
相关题目
20．
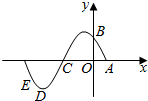已知A，B，C，D是函数f（x）=sin（ωx+φ）（ω＞0，0＜φ＜π）一个周期内的图象上的四个点，如图所示，$A（\frac{π}{6}，0）$，B为y轴上的点，D为图象上的最低点，C为该函数图象的一个对称中心，B与E关于点C对称，$\overrightarrow{ED}$在x轴上的投影为$\frac{π}{12}$，则$f（-\frac{π}{6}）$的值为（ ）
已知A，B，C，D是函数f（x）=sin（ωx+φ）（ω＞0，0＜φ＜π）一个周期内的图象上的四个点，如图所示，$A（\frac{π}{6}，0）$，B为y轴上的点，D为图象上的最低点，C为该函数图象的一个对称中心，B与E关于点C对称，$\overrightarrow{ED}$在x轴上的投影为$\frac{π}{12}$，则$f（-\frac{π}{6}）$的值为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{3}}}{2}$ | C． | $-\frac{1}{2}$ | D． | $-\frac{{\sqrt{3}}}{2}$ |
20．已知a∈R，则“|a-1|+|a|≤1”是“函数y=ax在R上为减函数”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |