题目内容
试讨论函数f(x)=loga (a>0且a≠1)在(1,+∞)上的单调性,并予以证明.
(a>0且a≠1)在(1,+∞)上的单调性,并予以证明.
解:设u= ,任取x2>x1>1,则
,任取x2>x1>1,则
u2-u1=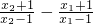
=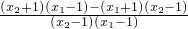
=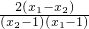 .
.
∵x1>1,x2>1,∴x1-1>0,x2-1>0.
又∵x1<x2,∴x1-x2<0.
∴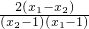 <0,即u2<u1.
<0,即u2<u1.
当a>1时,y=logax是增函数,∴logau2<logau1,
即f(x2)<f(x1);
当0<a<1时,y=logax是减函数,∴logau2>logau1,
即f(x2)>f(x1).
综上可知,当a>1时,f(x)=loga 在(1,+∞)上为减函数;
在(1,+∞)上为减函数;
当0<a<1时,f(x)=loga 在(1,+∞)上为增函数.
在(1,+∞)上为增函数.
分析:将函数f(x)看作是由y=logau和u= 两个函数复合而来,先证用单调性定义证明u=
两个函数复合而来,先证用单调性定义证明u= 的单调性,再用复合函数单调性的结论(同增异减)得到结论.
的单调性,再用复合函数单调性的结论(同增异减)得到结论.
点评:本题主要考查复合函数的单调性,要注意定义域.
 ,任取x2>x1>1,则
,任取x2>x1>1,则u2-u1=
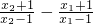
=
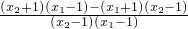
=
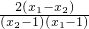 .
.∵x1>1,x2>1,∴x1-1>0,x2-1>0.
又∵x1<x2,∴x1-x2<0.
∴
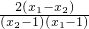 <0,即u2<u1.
<0,即u2<u1.当a>1时,y=logax是增函数,∴logau2<logau1,
即f(x2)<f(x1);
当0<a<1时,y=logax是减函数,∴logau2>logau1,
即f(x2)>f(x1).
综上可知,当a>1时,f(x)=loga
 在(1,+∞)上为减函数;
在(1,+∞)上为减函数;当0<a<1时,f(x)=loga
 在(1,+∞)上为增函数.
在(1,+∞)上为增函数.分析:将函数f(x)看作是由y=logau和u=
 两个函数复合而来,先证用单调性定义证明u=
两个函数复合而来,先证用单调性定义证明u= 的单调性,再用复合函数单调性的结论(同增异减)得到结论.
的单调性,再用复合函数单调性的结论(同增异减)得到结论.点评:本题主要考查复合函数的单调性,要注意定义域.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目