题目内容
已知函数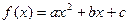
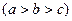 ,点
,点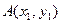 、
、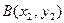 是该函数图象上的两点,且满足
是该函数图象上的两点,且满足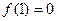 ,
,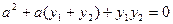 ;
;
(1)、求证: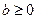 ;
;
(2)、问是否能够保证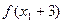 和
和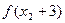 中至少有一个为正数?请证明你的结论。
中至少有一个为正数?请证明你的结论。
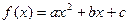
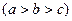 ,点
,点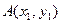 、
、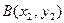 是该函数图象上的两点,且满足
是该函数图象上的两点,且满足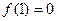 ,
,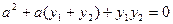 ;
;(1)、求证:
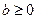 ;
;(2)、问是否能够保证
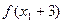 和
和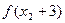 中至少有一个为正数?请证明你的结论。
中至少有一个为正数?请证明你的结论。(1)见解析(2)见解析
(1)、依题意,有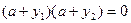 ,则
,则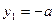 或
或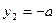 ,
,
则方程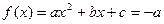 有实根,即方程
有实根,即方程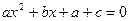 有实根,
有实根,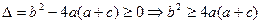 ,
,
又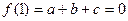 且
且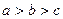 ,则
,则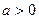 、
、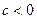 、
、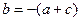 ,
,
则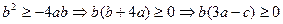 ,
,
由于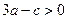 ,则
,则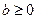 ;
;
(2)、依题意,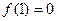 ,即1是方程
,即1是方程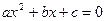 的一个根,则另一个根为
的一个根,则另一个根为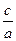 ,且
,且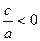 ,则有
,则有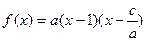 ,不妨设
,不妨设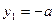 ,
,
即: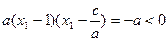 ,∴
,∴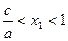 ,∴
,∴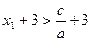 (◆)
(◆)
又由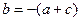 及
及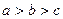 得
得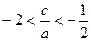 ,
,
∴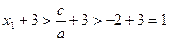 ,
,
而函数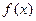 在
在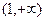 上为增函数,∴
上为增函数,∴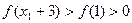 ,
,
同理,若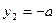 ,则有
,则有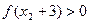 ,命题得证。
,命题得证。
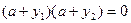 ,则
,则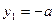 或
或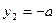 ,
,则方程
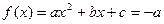 有实根,即方程
有实根,即方程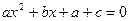 有实根,
有实根,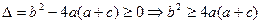 ,
,又
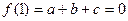 且
且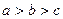 ,则
,则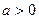 、
、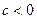 、
、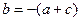 ,
,则
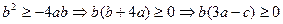 ,
,由于
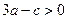 ,则
,则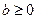 ;
;(2)、依题意,
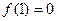 ,即1是方程
,即1是方程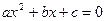 的一个根,则另一个根为
的一个根,则另一个根为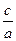 ,且
,且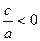 ,则有
,则有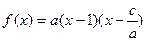 ,不妨设
,不妨设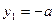 ,
,即:
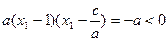 ,∴
,∴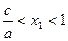 ,∴
,∴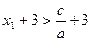 (◆)
(◆)又由
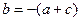 及
及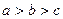 得
得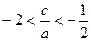 ,
,∴
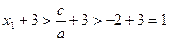 ,
,而函数
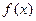 在
在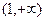 上为增函数,∴
上为增函数,∴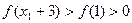 ,
,同理,若
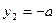 ,则有
,则有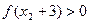 ,命题得证。
,命题得证。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
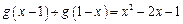 ,且
,且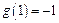 .令
.令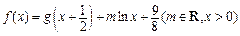 .
.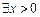 使
使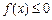 成立,求实数m的取值范围;
成立,求实数m的取值范围;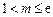 ,
,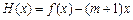 ,证明:对
,证明:对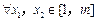 ,恒有
,恒有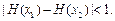
 ,若
,若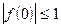 ,
, ,
,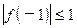 , 试证明:对于任意
, 试证明:对于任意 ,有
,有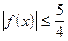 .
.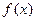 对任意的
对任意的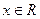 都有
都有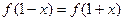 ,设向量
,设向量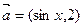 ,
,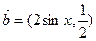 ,
,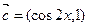 ,
,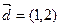 ,当
,当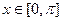 时,求
时,求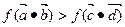 解集
解集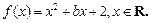
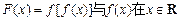 时有相同的值域,求b的取值范围;
时有相同的值域,求b的取值范围;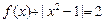 在(0,2)上有两个不同的根x1、x2,求b的取值范围,并证明
在(0,2)上有两个不同的根x1、x2,求b的取值范围,并证明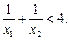
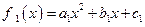 和
和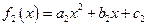 使得
使得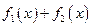 在
在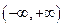 上是增函数的条件是__________________.
上是增函数的条件是__________________.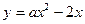 图像上有且仅有两个点到x轴的距离等于1,则a的取值范围是 _______ .
图像上有且仅有两个点到x轴的距离等于1,则a的取值范围是 _______ .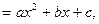 若a,b,c成等比,
若a,b,c成等比,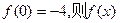 有最 值且该值为
有最 值且该值为