题目内容
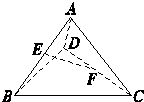
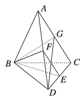
如图所示,在空间四边形ABCD中,各边长及对角线长都是a,点M、N分别是BC、AD的中点,求异面直线CN、DM所成角的余弦.

答案:
解析:
提示:
解析:
|
解:连结BN,取BN的中点,连结ME、DE.∵点M为BC的中点,∴ME∥CN,且ME= ∵EN= ∴DE= 在△DME中,∵ME= ∴cos∠DME= 即异面直线CN和DM所成角的余弦值为 |
提示:
|
求异面直线所成的角关键是选择一个“恰当的点”,通过“恰当的点”平移直线,找到异面直线所成的角或它的补角,再通过解三角形求解. |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 .
.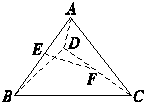 如图所示,在空间四边形ABCD中,E,F分别是AB,CD的中点,请判断向量
如图所示,在空间四边形ABCD中,E,F分别是AB,CD的中点,请判断向量 ,且AD⊥BC,对角线BD=
,且AD⊥BC,对角线BD= ,AC=
,AC= ,求AC和BD所成的角的大小.
,求AC和BD所成的角的大小.