题目内容
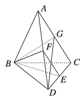
如图所示，在空间四边形ABCD中，E，F分别是AB，CD的中点，请判断向量| EF |
| AD |
| BC |
分析：取AC中点为G，连接EG，FG，利用三角形的中位线定理可知
=
，
=
，由
，
，
共面即可判断向量
与
+
是否共线．
| GF |
| 1 |
| 2 |
| AD |
| EG |
| 1 |
| 2 |
| BC |
| GF |
| EG |
| EF |
| EF |
| AD |
| BC |
解答：解：取AC中点为G，连接EG，FG，
∴
=
，
=
，
又∵
，
，
共面，
∴
=
+
=
+
=
（
+
），
∴
与
+
共线．
∴
| GF |
| 1 |
| 2 |
| AD |
| EG |
| 1 |
| 2 |
| BC |
又∵
| GF |
| EG |
| EF |
∴
| EF |
| EG |
| GF |
=
| 1 |
| 2 |
| AD |
| 1 |
| 2 |
| BC |
=
| 1 |
| 2 |
| AD |
| BC |
∴
| EF |
| AD |
| BC |
点评：本题考查向量共线，考查三角形的中位线定理，考查推理证明能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
。求异面直线AB与CD所成的角。
，且AD⊥BC，对角线BD=
，AC=
，求AC和BD所成的角的大小．
