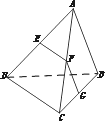
题目内容
如图所示,在空间四边形ABCD中,已知AD=1,BC= ,且AD⊥BC,对角线BD=
,且AD⊥BC,对角线BD= ,AC=
,AC= ,求AC和BD所成的角的大小.
,求AC和BD所成的角的大小.
 ,且AD⊥BC,对角线BD=
,且AD⊥BC,对角线BD= ,AC=
,AC= ,求AC和BD所成的角的大小.
,求AC和BD所成的角的大小.
| 解:如图所示,分别取AD,CD,AB,DB的中点E,F,G,H, 连结EF,FH,HG,GE,GF, 则由三角形中位线定理知EF∥AC且EF=  GE∥BD且GE=  GH∥AD,GH=  HF∥BC,HF=  从而可知GE与EF所成的锐角(或直角)即为AC和BD所成的角, GH和HF所成的锐角(或直角)即为AD与BC所成的角, ∵AD⊥BC, ∴∠GHF=90°, ∴GF2=GH2+HF2=1, 在△EFG中,EG2+EF2=1=GF2, ∴∠GEF=90°,即AC与BD所成的角为90°。 |
 |

练习册系列答案
相关题目