题目内容
化简；
（1）cosθ•tanθ；
（2）（1-sinθ）（1+sinθ）．
（1）cosθ•tanθ；
（2）（1-sinθ）（1+sinθ）．
考点：三角函数的化简求值
专题：三角函数的求值
分析：利用三角函数间的关系式，分别对（1）（2）化简即可．
解答：
解：（1）cosθ•tanθ=cosθ•
=sinθ；
（2）（1-sinθ）（1+sinθ）=1-sin2θ=cos2θ．
| sinθ |
| cosθ |
（2）（1-sinθ）（1+sinθ）=1-sin2θ=cos2θ．
点评：本题考查三角函数的化简求值，属于基础题．
练习册系列答案
相关题目
在等比数列{an}中，若a1，a10是方程3x2-2x-6=0的两根，则a4•a7=（ ）
| A、-6 | ||
| B、-2 | ||
| C、2 | ||
D、
|
下列命题中正确的是（ ）
A、x+
| ||||
B、
| ||||
C、
| ||||
D、6─x─
|
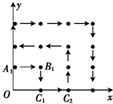为防洪抗旱，某地区大面积植树造林，如图，在区域{（x，y）|x≥0，y≥0}内植树，第一棵树在A1（0，1）点，第二棵树在B1（1，1）点，第三棵树在C1（1，0）点，第四棵树在C2（2，0）点，接着按图中箭头方向每隔一个单位长度种一棵树，那么，坐标为（43，0）的点是第等比数列{an}中，前n项和Sn=
+x，则x的值为（ ）
| 2n |
| 4 |
A、-
| ||
| B、-4 | ||
| C、-1 | ||
| D、4 |
要得到函数y=cos
x的图象，只要将函数y=cos（
x+1）的图象（ ）
| 1 |
| 2 |
| 1 |
| 2 |
| A、向左平移2个单位 | ||
| B、向右平移2个单位 | ||
C、向左平移
| ||
D、向右平移
|