题目内容
已知z是复数,z+2i, 均为实数(i为虚数单位),且复数(z+ai)2在复平面上对应的点在第一象限,求实数a的取值范围.
均为实数(i为虚数单位),且复数(z+ai)2在复平面上对应的点在第一象限,求实数a的取值范围.
.解:设z=x+yi(x,y∈R),
则z+2i=x+(y+2)i,
由题意得y=-2.
∵ =
= (x-2i)(2+i)
(x-2i)(2+i)
= (2x+2)+
(2x+2)+ (x-4)i.
(x-4)i.
由题意得x=4,∴z=4-2i.
∴(z+ai)2=(12+4a-a2)+8(a-2)i.
由于(z+ai)2在复平面上对应的点在第一象限,∴ 解得2<a<6.
解得2<a<6.
∴实数a的取值范围是(2,6).

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 ,n=
,n= ,点P(x,y)在y=sin x的图像上运动.Q是函数y=f(x)图像上的点,且满足
,点P(x,y)在y=sin x的图像上运动.Q是函数y=f(x)图像上的点,且满足 =m⊗
=m⊗ +n(其中O为坐标原点),则函数y=f(x)的值域是________.
+n(其中O为坐标原点),则函数y=f(x)的值域是________.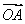 ,
,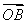 ,
, ,
, 满足等式
满足等式 ,则四边形ABCD的面积为________.
,则四边形ABCD的面积为________. =________.
=________. ,记数列{an}的前n项之积为Tr,则T2 013的值为( )
,记数列{an}的前n项之积为Tr,则T2 013的值为( ) B.-1
B.-1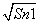 -Sn-1
-Sn-1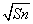 =2
=2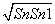 (n∈N*且n≥2),则a81=( )
(n∈N*且n≥2),则a81=( ) 过一、三象限的渐近线平行且距离为
过一、三象限的渐近线平行且距离为 的直线方程为 .
的直线方程为 .