题目内容
已知数列{an}的通项公式为an=n2-21n+20.
(1)n为何值时,an有最小值?并求出最小值;
(2)n为何值时,该数列的前n项和最小?
解:(1)因为an=n2-21n+20= 2-
2- ,可知对称轴方程为n=
,可知对称轴方程为n= =10.5.又因n∈N*,故n=10或n=11时,an有最小值,其最小值为112-21×11+20=-90.
=10.5.又因n∈N*,故n=10或n=11时,an有最小值,其最小值为112-21×11+20=-90.
(2)设数列的前n项和最小,则有an≤0,由n2-21n+20≤0,解得1≤n≤20,故数列{an}从第21项开始为正数,所以该数列的前19或20项和最小.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
 B.
B.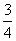
 D.
D.
 的模为________.
的模为________. 均为实数(i为虚数单位),且复数(z+ai)2在复平面上对应的点在第一象限,求实数a的取值范围.
均为实数(i为虚数单位),且复数(z+ai)2在复平面上对应的点在第一象限,求实数a的取值范围. ≤2的正整数n的集合为( )
≤2的正整数n的集合为( ) 的小正方形,在其上用粗线画出了一四棱锥的三视图,则该四棱锥的体积为( )
的小正方形,在其上用粗线画出了一四棱锥的三视图,则该四棱锥的体积为( ) B.
B. C.
C. D.
D.

 中,
中, ,
, ,
, 为
为 的中点,
的中点, 为
为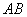 的中点,且
的中点,且 为正三角形.
为正三角形. 平面
平面 ;
; ,
, ,求点
,求点 到平面
到平面 的距离.
的距离.
 =3,n∈N*,若数列{cn}满足cn=ban,则c2 013=( )
=3,n∈N*,若数列{cn}满足cn=ban,则c2 013=( ) 、
、 均为单位向量,它们的夹角为
均为单位向量,它们的夹角为 ,那么
,那么 ( )
( ) B.
B. C.
C. D.
D.