题目内容
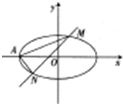
已知椭圆E的方程为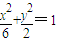 ,其左焦点为F,点M(-3,0),过点F的直线(不垂直于坐标轴)与E交于A,B两点.
,其左焦点为F,点M(-3,0),过点F的直线(不垂直于坐标轴)与E交于A,B两点.(I)证明:∠AMF=∠FMB;
(II)求△MAB面积S的最大值.
【答案】分析:(I) 由 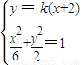 可得 (1+3k2)x2+12k2 x+12k2-6=0,求出x1+x2 和x1•x2
可得 (1+3k2)x2+12k2 x+12k2-6=0,求出x1+x2 和x1•x2
的值,求得AM 和BM 的斜率之和 KAM+KBM=0,从而得到∠AMF=∠FMB 成立.
(II)由△MAB面积S= MF•|y1-y2|=
MF•|y1-y2|=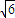 •
•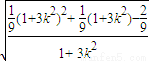 ,令 t=1+3k2,t≥1 得S=
,令 t=1+3k2,t≥1 得S=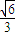 •
•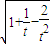 ≤
≤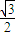 ,从而得出结论.
,从而得出结论.
解答:解:(I)证明:根据题意,设AB的直线方程为 y=k(x+2),k≠0,A (x1,y1 ),B(x2,y2),
由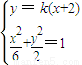 可得 (1+3k2)x2+12k2 x+12k2-6=0,
可得 (1+3k2)x2+12k2 x+12k2-6=0,
∴x1+x2=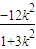 ,x1•x2=
,x1•x2=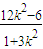 ,
,
∴KAM+KBM=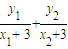 =
=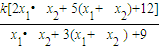 ,
,
∴2x1•x2+5(x1+x2)+12=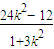 +
+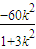 +12=0,
+12=0,
∴∠AMF=∠FMB 成立.
(II)求△MAB面积S= MF•|y1-y2|=
MF•|y1-y2|= •|k|•
•|k|•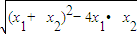
=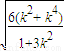 =
=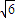 •
•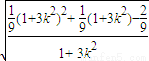 .
.
令 t=1+3k2,t≥1,则 S=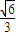 •
•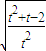 =
=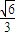 •
•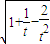 ≤
≤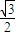 ,
,
故△MAB面积S的最大值等于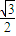 .
.
点评:本题考查直线的斜率公式,直线和圆锥曲线的位置关系,弦长公式的应用,得到△MAB面积S=
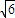 •
•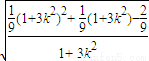 ,是解题的难点.
,是解题的难点.
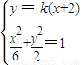 可得 (1+3k2)x2+12k2 x+12k2-6=0,求出x1+x2 和x1•x2
可得 (1+3k2)x2+12k2 x+12k2-6=0,求出x1+x2 和x1•x2 的值,求得AM 和BM 的斜率之和 KAM+KBM=0,从而得到∠AMF=∠FMB 成立.
(II)由△MAB面积S=
 MF•|y1-y2|=
MF•|y1-y2|=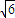 •
•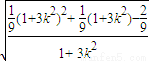 ,令 t=1+3k2,t≥1 得S=
,令 t=1+3k2,t≥1 得S=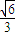 •
•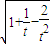 ≤
≤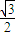 ,从而得出结论.
,从而得出结论.解答:解:(I)证明:根据题意,设AB的直线方程为 y=k(x+2),k≠0,A (x1,y1 ),B(x2,y2),
由
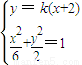 可得 (1+3k2)x2+12k2 x+12k2-6=0,
可得 (1+3k2)x2+12k2 x+12k2-6=0,∴x1+x2=
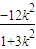 ,x1•x2=
,x1•x2=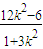 ,
,∴KAM+KBM=
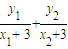 =
=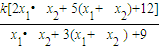 ,
,∴2x1•x2+5(x1+x2)+12=
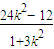 +
+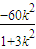 +12=0,
+12=0,∴∠AMF=∠FMB 成立.
(II)求△MAB面积S=
 MF•|y1-y2|=
MF•|y1-y2|= •|k|•
•|k|•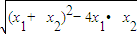
=
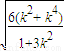 =
=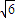 •
•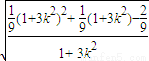 .
.令 t=1+3k2,t≥1,则 S=
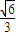 •
•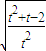 =
=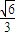 •
•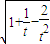 ≤
≤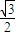 ,
,故△MAB面积S的最大值等于
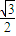 .
.点评:本题考查直线的斜率公式,直线和圆锥曲线的位置关系,弦长公式的应用,得到△MAB面积S=
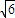 •
•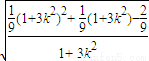 ,是解题的难点.
,是解题的难点. 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知椭圆E的方程为:
已知椭圆E的方程为: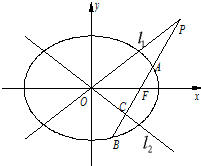 已知椭圆E的方程为
已知椭圆E的方程为 (2012•闵行区一模)已知椭圆E的方程为
(2012•闵行区一模)已知椭圆E的方程为