题目内容
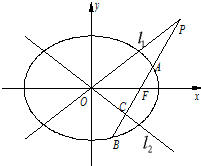 已知椭圆E的方程为
已知椭圆E的方程为| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
(1)当直线l1的倾斜角为30°,双曲线的焦距为8时,求椭圆的方程;
(2)设
| PA |
| AF |
| PB |
| BF |
分析:(1)因为直线l1的倾斜角为30°,所以
=
,因为双曲线的焦距为8,所以c=4再根据a,b,c关系,可得椭圆方程.
(2)由l⊥l2于点C,以及l1和l2方程可得出l方程,再与l1方程联立,求出P点坐标.再设出A,B坐标,由
=λ1
,
=λ2
,计算出λ1+λ2,的值即可.
| b |
| a |
| ||
| 3 |
(2)由l⊥l2于点C,以及l1和l2方程可得出l方程,再与l1方程联立,求出P点坐标.再设出A,B坐标,由
| PA |
| AF |
| PB |
| BF |
解答:解:(1)由已知,
=
,a2+b2=16.
解得:a2=12,b2=4
所以椭圆E的方程是
+
=1
(2)解法1:设A(x1,y1),B(x2,y2)
由题意得:直线l1的方程为:y=
x,直线l2的方程为:y=-
x
则直线l的方程为:y=
(x-c),其中点F的坐标为(c,0);
由
得:
,则点P(
,
)
由
消y得:2x2-2cx+(c2-a2)=0,则x1+x2=c x1x2=
;
由
= λ1
得:x1-
=λ1(c-x2),则:λ1=
,
同理由
=λ2
得:λ2=
.
λ1+λ2=
+
=
=
=0
故λ1+λ2=0为常数.
解法2:过p作X轴的垂线M,过A,B分别作m的垂线,垂足分别为A1,B1
由题意得:直线l1的方程为:y=
x,直线l2的方程为:y=-
x
则直线l的方程为:y=
(x-c),其中点F的坐标为(c,0)
由
得:
,则直线m为椭圆E的右准线
则:
=
,
=
,其中e的离心率
λ1=
,λ2=-
,
=
,故λ1+λ2=0
∴λ1+λ2为常数
| b |
| a |
| ||
| 3 |
解得:a2=12,b2=4
所以椭圆E的方程是
| x2 |
| 12 |
| y2 |
| 4 |
(2)解法1:设A(x1,y1),B(x2,y2)
由题意得:直线l1的方程为:y=
| b |
| a |
| b |
| a |
则直线l的方程为:y=
| a |
| b |
由
|
|
| a2 |
| c |
| ab |
| c |
由
|
| c2-a2 |
| 2 |
由
| PA |
| AF |
| a2 |
| c |
| cx1-a2 |
| c(c-x1)) |
同理由
| PA |
| BF |
| cx1-a2 |
| c(c-x2) |
λ1+λ2=
| cx1-a2 |
| c(c-x1)) |
| cx2-a2 |
| c(c-x2)) |
| (cx1-a2)(c-x2)+(cx2-a2)(c-x1) |
| c(c-x1))(c-x2)) |
| (c2+a2 )c-c(c2-a2)-2ca2 |
| c(c-x1))(c-x2) |
故λ1+λ2=0为常数.
解法2:过p作X轴的垂线M,过A,B分别作m的垂线,垂足分别为A1,B1
由题意得:直线l1的方程为:y=
| b |
| a |
| b |
| a |
则直线l的方程为:y=
| a |
| b |
由
|
|
则:
| ||
|
|
| ||
e|
|
| ||
|
|
| ||
e|
|
λ1=
|
| ||
|
|
|
| ||
|
|
|
| ||
|
|
|
| ||
|
|
∴λ1+λ2为常数
点评:本题考查了椭圆,双曲线与直线的位置关系,计算量较大,须认真解答.

练习册系列答案
相关题目
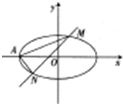 已知椭圆E的方程为:
已知椭圆E的方程为:
 +
+ =1(a>b>0)的右焦点坐标为(1,0),点P(1,
=1(a>b>0)的右焦点坐标为(1,0),点P(1, )在椭圆E上.
)在椭圆E上.