题目内容
16.定义在R上的奇函数f(x)在区间(-∞,0)上单调递减,且f(2)=0,则不等式xf(x-1)≥0的解集为[-1,0]∪[1,3].分析 根据奇函数的性质求出f(-2)=0,由条件画出函数图象示意图,结合图象并对x分类列出不等式组,分别利用函数的单调性求解即可求出不等式的解集.
解答 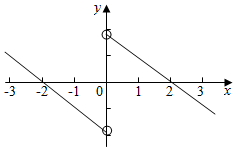 解:∵f(x)为奇函数,且f(2)=0,在(-∞,0)是减函数,
解:∵f(x)为奇函数,且f(2)=0,在(-∞,0)是减函数,
∴f(-2)=-f(2)=0,f(x)在(0,+∞)内是减函数,
函数图象示意图:其中f(0)=0,
∵xf(x-1)≥0,
∴$\left\{\begin{array}{l}{x≤0}\\{f(x-1)≤0}\end{array}\right.$或$\left\{\begin{array}{l}{x>0}\\{f(x-1)≥0}\end{array}\right.$,
解得-1≤x≤0或1≤x≤3,
∴不等式的解集是[-1,0]∪[1,3],
故答案为:[-1,0]∪[1,3].
点评 本题考查函数的奇偶性、单调性的综合应用,正确画出函数的示意图是解题的关键,考查分类讨论思想和数形结合思想.

练习册系列答案
相关题目
6.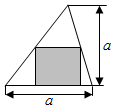 在底和高等长度的锐角三角形中有一个内接矩形,矩形的一边在三角形的底边上,如图,在三角形内取一点,则该点落入矩形内的最大概率为( )
在底和高等长度的锐角三角形中有一个内接矩形,矩形的一边在三角形的底边上,如图,在三角形内取一点,则该点落入矩形内的最大概率为( )
 在底和高等长度的锐角三角形中有一个内接矩形,矩形的一边在三角形的底边上,如图,在三角形内取一点,则该点落入矩形内的最大概率为( )
在底和高等长度的锐角三角形中有一个内接矩形,矩形的一边在三角形的底边上,如图,在三角形内取一点,则该点落入矩形内的最大概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
6.已知{an}是等差数列,Sn为其前n项和,若正整数i,j,k,l满足i≤k≤l≤j,且i+j=k+l,则( )
| A. | aiaj≤akal | B. | aiaj≥akal | C. | SiSj<SkSl | D. | SiSj≥SkSl |
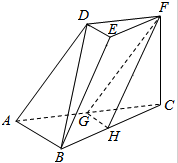 如图,三棱台DEF-ABC中,底面是以AB为斜边的直角三角形,FC⊥底面ABC,AB=2DE,G,H分别为AC,BC的中点.
如图,三棱台DEF-ABC中,底面是以AB为斜边的直角三角形,FC⊥底面ABC,AB=2DE,G,H分别为AC,BC的中点.