题目内容
11.已知程序框图如图,则输出的i=( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
分析 由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量S的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.
解答 解:当S=1时,满足进行循环的条件,则S=$\sqrt{3}$,i=5,
当S=$\sqrt{3}$时,满足进行循环的条件,则S=$\sqrt{\sqrt{3}×5}$,i=7,
当S=$\sqrt{\sqrt{3}×5}$时,满足进行循环的条件,则S=$\sqrt{\sqrt{\sqrt{3}×5}×7}$,i=9,
当S=$\sqrt{\sqrt{\sqrt{3}×5}×7}$≈4.539时,不满足进行循环的条件,
故输出的i值为9,
故选:C
点评 本题考查的知识点是程序框图,当循环的次数不多,或有规律时,常采用模拟循环的方法解答.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
2.北京时间3月4日,CBA半决赛第四场,辽宁男篮客场战胜广东,总比分3:1淘汰对手紧急总决赛,辽宁与四川会师决赛,总决赛3月11日开打,采用7局4胜制(若某队取胜四场,则终止比赛,并获得本赛季冠军)采用2-3-2的赛程,由于辽宁常规赛占优,决赛时拥有主场优势(辽宁先两个主场,然后三个客场,再两个主场)以下是总决赛赛程:
(1)若考虑主场优势,每个队主场获胜的概率均为$\frac{2}{3}$,客场取胜的概率均为$\frac{1}{3}$,求辽宁队以比分4:1获胜的概率;
(2)若不考虑主场优势,每个队每场比赛获胜的概率均为$\frac{1}{2}$设本次决赛的比赛场数为X,求X的分布列及数学期望.
| 日期 | 比赛队 | 主场 | 客场 | 比赛时间 | 比赛地点 |
| 3月11日 | 辽宁-四川 | 辽宁 | 四川 | 19:35 | 本溪 |
| 3月13日 | 辽宁-四川 | 辽宁 | 四川 | 19:35 | 本溪 |
| 3月16日 | 四川-辽宁 | 四川 | 辽宁 | 19:35 | 成都 |
| 3月18日 | 四川-辽宁 | 四川 | 辽宁 | 19:35 | 成都 |
| 3月20日 | 四川-辽宁 | 四川 | 辽宁 | 19:35 | 成都 |
| 3月23日 | 辽宁-四川 | 辽宁 | 四川 | 19:35 | 本溪 |
| 3月25日 | 辽宁-四川 | 辽宁 | 四川 | 19:35 | 本溪 |
(2)若不考虑主场优势,每个队每场比赛获胜的概率均为$\frac{1}{2}$设本次决赛的比赛场数为X,求X的分布列及数学期望.
1.已知点P为函数f(x)=lnx的图象上任意一点,点Q为圆[x-(e+$\frac{1}{e}$)]2+y2=1任意一点,则线段PQ的长度的最小值为( )
| A. | $\frac{e-\sqrt{{e}^{2}-1}}{e}$ | B. | $\frac{\sqrt{2{e}^{2}+1}-e}{e}$ | C. | $\frac{\sqrt{{e}^{2}+1}-e}{e}$ | D. | e+$\frac{1}{e}$-1 |
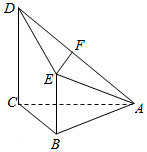 如图,四棱锥A-BCDE中,AB=BCC,BE=$\frac{1}{2}$CD.CD⊥面ABC,BE∥CD,F为AD的中点.
如图,四棱锥A-BCDE中,AB=BCC,BE=$\frac{1}{2}$CD.CD⊥面ABC,BE∥CD,F为AD的中点.