题目内容
不等式:①a2+2>2a;②a2+b2≥2(a-b-1);③a2+b2≥ab恒成立的个数是( )
| A、0 | B、1 | C、2 | D、3 |
考点:基本不等式
专题:不等式的解法及应用
分析:利用“作差法”和实数的基本性质即可得出.
解答:
解:①a2+2-2a=(a-1)2+1≥1,∴a2+2>2a,正确;
②∵a2+b2-2(a-b-1)=(a-1)2+(b+1)2≥0,∴a2+b2≥2(a-b-1),正确;
③a2+b2-ab=(a-
b)2+
b2≥0,当且仅当a=b=0时取等号,正确.
综上可得:①②③都恒成立.
故选:D.
②∵a2+b2-2(a-b-1)=(a-1)2+(b+1)2≥0,∴a2+b2≥2(a-b-1),正确;
③a2+b2-ab=(a-
| 1 |
| 2 |
| 3 |
| 4 |
综上可得:①②③都恒成立.
故选:D.
点评:本题考查了“作差法”和实数的基本性质、不等式的性质,属于基础题.

练习册系列答案
相关题目
直线3x-2y-6=0在x轴上的截距为a,在y轴上的截距为b,则( )
| A、a=2,b=3 |
| B、a=-2,b=-3 |
| C、a=-2,b=3 |
| D、a=2,b=-3 |
执行如图所示的程序框图后,输出的值为4,则P的取值范围是( )


A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
设f(x)是定义在[-6,6]上的偶函数,且f(4)>f(1),则下列各式一定成立的是( )
| A、f(0)<f(6) |
| B、f(4)>f(3) |
| C、f(2)>f(0) |
| D、f(-1)<f(4) |
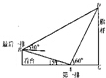 某中学举行升旗仪式,如图所示,在坡度为15°的看台上,从正对旗杆的一列的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离AB=10
某中学举行升旗仪式,如图所示,在坡度为15°的看台上,从正对旗杆的一列的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离AB=10