题目内容
(1）用综合法证明：
(
)
（2）用反证法证明：若
均为实数，且
，
，
求证：中至少有一个大于0.
（1）证明详见解析；（2）证明详见解析.
解析试题分析：（1）充分利用好基本不等式
得出、
、
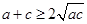，进而再利用同向不等式的可加性即可得到结论，注意关注等号成立的条件；（2）先设结论的反面成立即都不大于0，进而得出
，另一方面
，从而产生了矛盾，进而肯定假设不成立，可得原命题的结论成立.
(1)
1分
（当且仅当
时等号成立） ①（当且仅当
时等号成立） ②
（当且仅当
时等号成立） ③ 3分
所以①+②+③得
即
5分
当且仅当
时取等号 7分
(2) 假设都不大于0即
8分
根据同向不等式的可加性可得 ④ 11分
又
与④式矛盾
所以假设不成立即原命题的结论中至少有一个大于0 15分.
考点：1.综合法；2.反证法；3.基本不等式的应用.
练习册系列答案
阅读快车系列答案
相关题目
为三角形
的三边，求证：
中，
，且
成等差数列，
成等比数列
.
；
使得
对一切
恒成立？若存在，求出
；
，试用分析法证明：
.
，
，
，
，
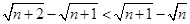，你能得到一个怎样的一般不等式？并加以证明．
.
, 
, 
, . . . . . .