题目内容
若函数 满足:集合
满足:集合 中至少存在三个不同的数构成等比数列,则称函数
中至少存在三个不同的数构成等比数列,则称函数 是等比源函数.
是等比源函数.
(1)判断下列函数:① ;②
;② 中,哪些是等比源函数?(不需证明)
中,哪些是等比源函数?(不需证明)
(2)证明:对任意的正奇数 ,函数
,函数 不是等比源函数;
不是等比源函数;
(3)证明:任意的 ,函数
,函数 都是等比源函数.
都是等比源函数.
(1)①②都是等比源函数;(2)参考解析;(3)参考解析
解析试题分析:(1)函数 满足:集合
满足:集合 中至少存在三个不同的数构成等比数列,则称函数
中至少存在三个不同的数构成等比数列,则称函数 是等比源函数.由等比源函数的定义可知.令x=2,4,16.即可得函数
是等比源函数.由等比源函数的定义可知.令x=2,4,16.即可得函数 对应的三项为等比数列.令x=1,3,5即可得函数
对应的三项为等比数列.令x=1,3,5即可得函数 对应的三项成等比数列.所以①②都是等比源函数.
对应的三项成等比数列.所以①②都是等比源函数.
(2)对任意的正奇数 ,函数
,函数 不是等比源函数,应用反正法,假设存在三项,根据奇偶性的性质即可得到假设不成立.从而得到证明.
不是等比源函数,应用反正法,假设存在三项,根据奇偶性的性质即可得到假设不成立.从而得到证明.
(3)函数 ,对任意的
,对任意的 是等比源函数.至少存在三个不同的数构成等比数列.通过证明存在三项.即命题成立.
是等比源函数.至少存在三个不同的数构成等比数列.通过证明存在三项.即命题成立.
试题解析:(1)①②都是等比源函数.4分
(2)证明:假设存在正整数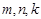 且
且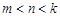 ,使得
,使得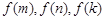 成等比数列,
成等比数列,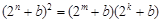 ,整理得
,整理得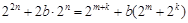 ,
,
等式两边同除以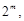 得
得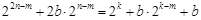 .
.
因为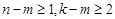 ,所以等式左边为偶数,等式右边为奇数,
,所以等式左边为偶数,等式右边为奇数,
所以等式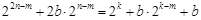 不可能成立,
不可能成立,
所以假设不成立,说明对任意的正奇数 ,函数
,函数 不是等比源函数10分
不是等比源函数10分
(3)因为任意的 ,都有
,都有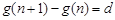 ,
,
所以任意的 ,数列
,数列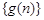 都是以
都是以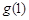 为首项公差为
为首项公差为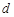 的等差数列.
的等差数列.
由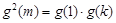 ,(其中
,(其中 )可得
)可得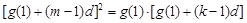 ,整理得
,整理得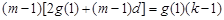 ,
,
令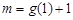 ,则
,则 ,
,
所以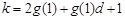 ,
,
所以任意的 ,数列
,数列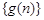 中总存在三项
中总存在三项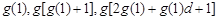 成等比数列.
成等比数列.
所以任意的 ,函数
,函数 都是等比源函数.18分
都是等比源函数.18分
考点:1.新定义函数的概念.2.列举递推的思想.3.反正法思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 则
则 ”类比“若
”类比“若 为三个向量则
为三个向量则 ”
” 中,
中, 猜想
猜想
 ,则
,则 .
. +
+ +…+
+…+ >
> 对一切正整数n都成立,猜想正整数a的最大值,并证明结论.
对一切正整数n都成立,猜想正整数a的最大值,并证明结论. ;
; 均为实数,且
均为实数,且 ,
, ,
,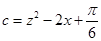 ,求证
,求证 ;
; ,试用分析法证明:
,试用分析法证明: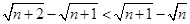 .
. ,那么x2+2x-1≠0.
,那么x2+2x-1≠0. ;
; ;
; ,
,