Question

给出关于函数f（x）=

1 6 x2+ 5 6 x，-5≤x＜3 10-2x，3≤x≤5

的下列结论：
①若实数a，b，c互不相同，且f（a）=f（b）=f（c）=d，则a+b+c+d=0；
②若f（x）≤k（x+5）对x∈[-5，5]恒成立，则k的值不可能小于

1

2

；
③满足“当x∈[m，n]（n＞m≥0）时f（x）相应的值域恰好也是[m，n]”的实数对（m，n）有且仅有4对．
以上结论中，正确结论的个数为（　　）

• A、0
• B、1
• C、2
• D、3

Answer 1

考点：分段函数的应用

专题：阅读型,函数的性质及应用

分析：画出函数f（x）的图象，观察图象，即可判断①；讨论x=-5，-5＜x＜3，3≤x≤5，通过参数分离，结合单调性求出最值即可；③讨论[m，n]为增区间或减区间，或有增有减，结合图象和函数值，即可得到答案．

解答： 解：画出函数f（x）的图象，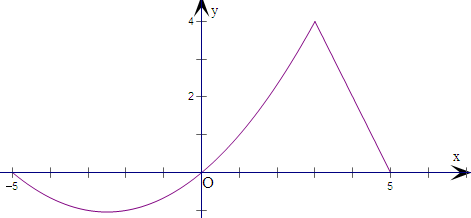
①若实数a，b，c互不相同，且f（a）=f（b）=f（c）=d，
由图象可知，
d=0，c=5，b=0，a=-5，
故a+b+c+d=0，
即①正确；
②若f（x）≤k（x+5）对x∈[-5，5]恒成立，
若x=-5，则f（-5）=0，k（x+5）=0，成立；
若-5＜x＜3，则

1

6

（x²+5x）≤k（x+5），即k≥

1

6

x，则有k≥

1

2

；
若3≤x≤5，则10-2x≤k（x+5），即k≥

2(5-x)

x+5

=

20

x+5

-2，
则有k≥

20

8

-2，即k≥

1

2

．故②正确；
③若[m，n]为增区间，则f（m）=m，f（n）=n，

1

6

（m²+5m）=m，

1

6

（n²+5n）=n，
解得m=0，n=1，若[m，n]为减区间，则f（m）=n，f（n）=m，推出m=n，不成立．
又f（4）=2，f（3）=4，故区间[0，4]，[1，4]也成立．故共有3个，即③错．
故选C．

点评：本题考查分段函数及运用，考查函数的单调性及运用，考查不等式的恒成立问题，转化为求最值问题，是一道综合题．